Les lois de probabilité telles que nous les connaissons prennent naissance durant la Renaissance. Mais il y a fort à parier que leur histoire débute durant l’Antiquité. Il était alors question de jeux de hasard, d’estimations marchandes incluant des périples dangereux ou encore de rentes viagères. Bien avant les lettres de Pascal à Fermat, les tavernes romaines devaient déjà raisonner des analyses statistiques avinées des joueurs de dés !
Comme nous l’avons vu dans le premier chapitre, les statistiques se divisent en deux grands domaines : les statistiques descriptives et les statistiques interférentielles. Dans le second cas, le statisticien parle communément d’inférence statistique. Les Lois de probabilité entrent en jeu dans la seconde catégorie et vont faciliter l’interprétation de variables aléatoires en sciences expérimentales.
Derrière ce jargon, nous sommes tout simplement dans l’idée que l’ensemble de la population N ne nous est pas accessible. Afin de connaître ses caractéristiques, nous allons étudier celles d’un échantillon n issu de cette population. L’inférence statistique consiste ensuite à induire les caractéristiques inconnues de la population N à partir de l’échantillon n.
Les caractéristiques de l’échantillon, une fois connues, reflètent alors avec une certaine marge d’erreur possible celles de la population. Pour appliquer cette méthode de raisonnement à une expérience, il nous faut donc connaître les Lois de Probabilité des variables aléatoires. Elles vont également s’appuyer sur le calcul de probabilités. Enfin rassurez-vous, nous ne piocherons dans le catalogue de lois disponibles que le strict minimum.

4. Les Lois de Probabilité
Pour illustrer les différentes lois de probabilité présentées ci-dessous, la distribution des densités de probabilité de chaque loi est réalisée avec le logiciel R v. 3.6.3.
4.1. Notions de probabilités
4.1.1. Déterminer une Loi de probabilité
En statistiques, une loi de probabilité est le comportement aléatoire d’un phénomène dépendant du hasard. Grâce à ces lois, il devient alors possible de modéliser des résultats inconnus d’avance, comme des phénomènes physiques, des observations biologiques ou des résultats économiques.
Une loi de probabilité d’une variable aléatoire X consiste donc à calculer la probabilité de tirage de l’ensemble des résultats contenus dans la variable aléatoire. Par exemple, considérons un lancer de dé à 6 faces. La variable aléatoire X prend alors 6 valeurs possibles et nous pouvons la considérer comme discrète.
- La loi uniforme discrète permet d’appliquer à ce phénomène dont les résultats sont équiprobables la probabilité P(Xn) = 1/n . Soit P = 1/6 pour un dé à 6 faces (n=6).
- La loi de Bernoulli permet de différencier deux issues possibles : succès et échec. Elles sont généralement codées comme chiffres binaires 0 et 1. Cette loi considère deux paramètres p,q servant à mesurer la probabilité de succès P(X=1) = p et d’échec P(X=0) = q . La somme des probabilités ∑P(X) = 1 ; ce qui permet d’établir que la probabilité q = 1 – p .
- La loi géométrique est la loi du temps d’attente du premier succès dans des épreuves de Bernoulli dans un tirage avec remise. Elle sert notamment pour la durée de vie d’un élément radioactif. Sa formulation : P(T=k) = p.qk-1
Pour une variable aléatoire dont nous connaissons les différentes valeurs, il est également possible de dresser un tableau de probabilités (voir l’exemple ci-dessous).
4.1.2. Exemple : un jeu d’argent pour tromper l’ennui
Pour animer les froides soirées d’affût photographique à loutre, des naturalistes décident de jouer à un petit jeu d’argent. Ils tirent alors à tour de rôle un dé à six faces et attribuent les scores suivants :
- Résultats de 1 : perd 5 euros
- Résultats impairs (3 et 5) : gagne 1 euro
- Résultat pairs (2 et 4) : perd 1 euro
- Résultat de 6 : gagne 5 euros
Soit X la variable aléatoire associée au gain ou à la perte d’argent. De plus, l’ensemble des valeurs xi de la variable aléatoire X ∈ {-5;-1;1;5}. Sachant cela, ils dressent alors un tableau de probabilités pour ce jeu de hasard :
| xi | -5 | -1 | +1 | +5 |
| P(X = xi) | 1/6 | 2/6 = 1/3 | 2/6 =1/3 | 1/6 |
On vérifie ensuite que ∑P(X) = 1/6 + 1/3 + 1/3 + 1/6 = 1 . Notre tableau de probabilités est donc complet. Si nous cherchons à savoir quelle est la probabilité de gagner 5 euros (succès), la loi de Bernoulli nous indique que p = 1/6 ; la probabilité de ne pas gagner le gain maximal (échec) vaut alors q = 1 – p = 5/6 .
De même en un seul tirage, la probabilité de gagner de l’argent (succès) vaut p = 1/3 + 1/6 = 1/2 et la probabilité de perdre de l’argent (échec) vaut q = 1 – p = 1/2. Soit une chance sur deux de se faire plumer en attendant que la loutre pointe le bout de sa moustache !
4.1.3. L’espérance mathématique
En probabilités, l’espérance mathématique d’une variable aléatoire discrète correspond à la valeur ou score attendu si l’on répète un grand nombre de fois la même expérience ou tirage. Pour rappel du chapitre 3, la formule mathématique est la suivante :

Dans l’exemple précédent, l’espérance mathématique du jeu de dés était donc de E = – 5x(1/6) – 1x(1/3) + 1x(1/3) + 5x(1/6) = 0 € . Cela signifie donc qu’en moyenne, les gains sont nuls au terme d’une soirée de jeu. Plutôt sympa pour un jeu amical, nos naturalistes peuvent espérer conserver leur argent en attendant la loutre. Mais à force de jouer au dé, ils risquent surtout de rater son passage !
4.2. La loi binomiale
4.2.1. Définition
Un grand classique des modèles de distribution d’une variable aléatoire discrète. Soit une variable aléatoire X comprenant k valeurs. Si l’on considère que le résultat de n tirages aléatoires avec remise suit une loi de Bernoulli, il en ressort alors que la probabilité d’obtenir la valeur k suit la formule :

Nous sommes donc en présence d’une loi binomiale B(n;p) où n est le nombre de tirages et p la probabilité de l’événement k étudié.
Pour comprendre comment fonctionne la loi binomiale, vous pouvez vous représenter un arbre de probabilités. Il permet de décrire l’ensemble des combinaisons d’événements à chaque tirage (avec remise). Dans la formule, la parenthèse permet d’additionner toutes les branches identiques de votre arbre. Il s’agit plus spécifiquement du nombre de combinaisons C et de ses coefficients binomiaux n et k.
Dans la loi de Bernoulli, chaque événement succès ou échec a une probabilité associée telle que ∑P(X) = p + q = 1 . Dans la loi binomiale, le tirage est répété n fois, de sorte que l’on considère combien de fois le succès est vérifié (valeur k). On met alors en exposant des probabilités cette répétition.
De plus, la moyenne µ d’une loi binomiale équivaut au calcul d’une espérance, soit µ = n.p . Enfin, la variance σ² de la loi binomiale vaut σ² = n.p.q .
4.2.2. Mise en situation de la loi binomiale
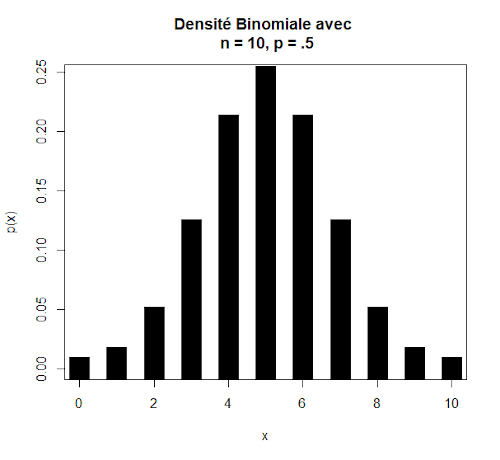
Par exemple, on cherche à savoir quelle est la probabilité de rencontrer k = 3 filles dans un groupe de n = 10 étudiants. Données : p =0,5 et q = 0,5 ; k = 3 et n – k = 7.
P(X=3) = C(103).(0,5)3.(0,5)7 = 120.(0,125).(0,0078) = 0,117
La densité binomiale ci-dessous permet de se figurer les probabilités respectives pour les différentes valeurs de k.
4.3. La loi de Pascal
La loi de Pascal ou loi binomiale négative s’applique pour une variable qui correspond au nombre de tirages successifs nécessaires pour obtenir r événements du même type. A l’inverse, la loi binomiale (positive) concerne le nombre d’événements du même type obtenus en n tirages. Par exemple, cette loi permet en biologie d’étudier les chances de capture de proies chez un prédateur.
4.4. La loi de Poisson
4.4.1. Définition
Une variable aléatoire discrète suit une loi de Poisson s’il faut effectuer un grand nombre de tirages pour observer les événements que l’on étudie. Il s’agit en effet de situations où la loi binomiale B(n;p) est affectée des conditions n → ∞ et p → 0. Pour ces limites, les valeurs k << n de telle sorte que le calcul du nombre de combinaisons donne des chiffres immenses !
Par exemple, nous cherchons la probabilité de trouver dans une population de n = 10.000 drosophiles un seul individu présentant une mutation rare (p = 0,001). La loi de Poisson s’applique alors à la situation. Pour cette raison, en biologie, la loi de Poisson est aussi appelée « Loi des événements rares« .
L’approximation binomiale par la loi de Poisson vient donc solutionner notre problème car sa formule approchée évite l’écueil mathématique d’un calcul de combinaisons trop « lourd ». Sa formule de paramètre λ = n.p est donnée ci-dessous :

Le paramètre λ = n.p correspond aussi à l’espérance de la loi. Comme la probabilité de succès p est très proche de 0, alors q = 1 – p ≈ 1. La variance s’approxime donc σ² = n.p.q ≈ n.p
4.4.2. Mise en application de la loi de Poisson
Pour se fixer des limites d’utilisation de cette loi, considérez que pour p < 0,1 et n > 30 vous pouvez utiliser la loi de Poisson. Par exemple, cherchons à caractériser le nombre possible de Merles noirs (Turdus merula) albinos (p = 10-4) dans une population de n = 10.000 individus, soit λ = 1.
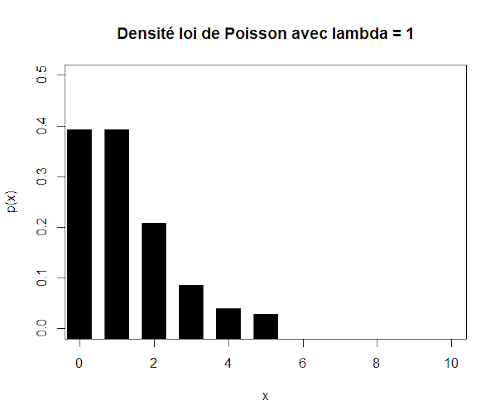
D’après cette distribution, la probabilité de rencontrer un Merle noir albinos chute brutalement selon une allure sigmoïde typique de la loi de Poisson.
4.5. La loi hypergéométrique
Cette loi s’applique aux variables aléatoires discrètes dans le cas d’un tirage aléatoire sans remise. Soit une population N dans laquelle un caractère spécifique subdivise des individus dans un sous-ensemble K. Nous effectuons n tirages, mais la probabilité de succès p ou d’échec q est modifiée après chaque tirage en l’absence de remise.
La loi hypergéométrique de paramètre H(A, Na, n) avec A le nombre total de boules, pA = Na le nombre de boules à succès, qA = A – Na et n le nombre de tirages indique que la probabilité P(k) d’obtenir k individus du sous-ensemble K se formule alors :

Par exemple, considérons un jeu de boules à piocher contenant N = 10 boules dont K = 4 boules noires. Nous effectuons 6 tirages. La loi hypergéométrique H(10, 4, 6) est la loi de la variable aléatoire X(k) qui compte les observations du caractère donné (les boules noires) dans un tirage sans remise. Sa distribution est la suivante :
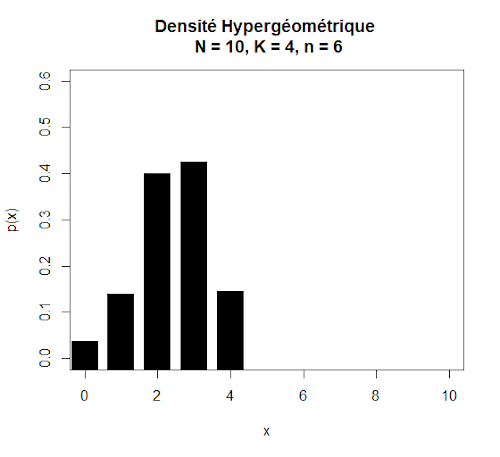
L’espérance d’une loi hypergéométrique vaut E(X) = n.p et la variance vaut V(X) = n.p.q.(N-n)/(N-1) . A noter également que la loi hypergéométrique peut aussi se noter de paramètre H(n, p, A).
Plus les valeurs de N et K sont grandes, plus la différence entre tirage avec ou sans remise s’amenuise. C’est pourquoi dans ce cas l’approximation par la loi binomiale de paramètre p = N/K est tout aussi valable.
4.6. La loi normale
4.6.1. Définitions
La loi normale s’applique pour des variables aléatoires continues dont les valeurs sont potentiellement infinies. En effet, les lois binomiales et de Poisson sont qualifiées de discrètes car elles s’appliquent à des valeurs entières et finies. Cela permet de calculer précisément la probabilité de succès d’un événement.
Dans le cas de mesures expérimentales (temps, masse, concentration, longueur, température, pH …) nous sommes en présences de variables aléatoires continues X dont les valeurs k possibles sont infinies, notamment en raison du degré de précision.
Nous allons donc calculer non pas une probabilité exacte pour une valeur k précise, mais la probabilité de X entre deux valeurs a et b. Pour se faire, il faut intégrer l’équation f(x) de la loi normale sur l’intervalle [a ; b].
Une loi normale N(µ;σ²) est une loi de probabilité continue qui dépend de son espérance notée μ et de son écart-type noté σ. La densité de probabilité de la loi normale d’espérance μ, et d’écart type σ est donnée par la formule suivante :

La courbe de cette densité de probabilité est appelée courbe de Gauss ou courbe en cloche.
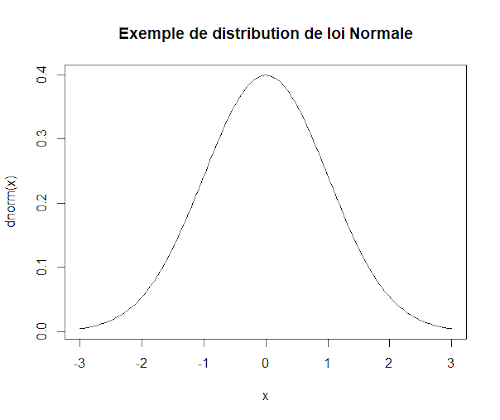
Lorsqu’une variable aléatoire continue X suit une loi normale, elle est dite gaussienne ou normale. On note alors que X ≈ N(µ;σ²). La loi normale de moyenne nulle et d’écart type unitaire est appelée loi normale centrée réduite ou loi normale standard.
4.6.2. Théorème central limite
Supposons tout d’abord que nous ayons à traiter n variables aléatoires : X1, X2, X3, … Xn. Elles sont indépendantes 2 à 2, distribuées selon la même densité de probabilité et possèdent toutes les mêmes moyenne et variance.
De plus, nous posons Sn = X1+ X2+ X3+ … + Xn de sorte que :


Alors Z tend vers une loi normale centrée-réduite N(0;1) lorsque n tend vers l’infini.
Conséquence du théorème central limite, la moyenne de cette somme µ(Sn) sera tout simplement égale à µ(Sn) = n.µ . La variance σ²(Sn) de cette somme sera égale à σ²(Sn) = n.σ² . Comme vu dans le chapitre 2, puisque Sn est une variable aléatoire, l’équation Zn correspond à une transformation de variables de type Y = a.X + b dans laquelle a = 1/(σ/√n) et b = -µ/(σ/√n) . Comme vu dans le chapitre 2, nous effectuons alors une opération de centrage-réduction de notre variable aléatoire Sn . Nous pouvons également définir une variable aléatoire Yi = (X̅n – µ)/σ pour laquelle µ = 0 et σ² = 1. Ce qui signifie que que pour Z :

Sa moyenne µ = 0 et sa variance σ² = 1 lorsque n tend vers l’infini. Elle suit donc bien une loi normale centrée réduite N(0;1).
4.6.3. Mise en situation du théorème central limite
Concrètement, quelle est la conséquence pour nos résultats expérimentaux ? Le théorème central limite s’applique à la somme de variables aléatoires indépendantes qui auraient toutes même moyenne et même variance. A première vue, cela signifie que nous aurions la chance infime de tomber une infinité de fois sur le même tirage aléatoire ! Ce qui bien entendu n’est pas le cas supposé ici.
Mais en réalité, la même conclusion se retrouve très souvent en sciences expérimentales. Prenons une population de 100 Piérides du navet (Peris napi) dont nous mesurons la longueur des ailes antérieures. A chaque capture (tirage aléatoire) d’un individu, nous effectuons notre mesure. Nous répétons l’opération capture après capture. A chaque fois, nous effectuons une moyenne de la même variable aléatoire « longueur de l’aile antérieure ».
Chacune des valeurs de longueur des ailes est inconnue à l’avance et à priori indépendantes entre-elles. Cependant, nous pouvons affirmer qu’elles ont toutes la même densité de probabilité, puisque issues de la même population de Piérides du navet. Chaque variable aléatoire aura la même moyenne µ et la même variance σ². Pour calculer la moyenne de la longueur de l’aile antérieure au sein de notre population, nous additionnons n variables aléatoires indépendantes distribuées selon la même densité de probabilité, de même moyenne et de même variance. Nous sommes donc bien dans les conditions du théorème central limite.

4.6.4. Libertés d’application du théorème central limite
Le théorème central limite n’est valable que si n tend vers l’infini. Or dans la pratique, il est démontré que ce théorème est vérifié dès lors que n > 30 . Cette approximation est largement répandue dans les sciences expérimentales.
De même, les statisticiens ont également démontré que ce théorème reste valable si la moyenne et la variance des variables aléatoires sont faiblement différentes entre-elles. Ce qui simplifie la comparaison au modèle en sciences expérimentales !
Enfin, sachez que l’indépendance entre deux variables aléatoires peut être partiellement remise en cause par approximation du théorème central limite. Une excellente nouvelle en biologie, puisque nos mesures d’individus au sein d’une population risquent forcément de suivre un certain degré de dépendance !
Quelle est la suite ? Dans l’épisode V, nous contre-attaquerons avec les lois des grands nombres. Une tranche plus théorique de statistiques, mais pourtant indispensable à la compréhension des intervalles de confiance.





