L’écologie utilise différents descripteurs statistiques pour caractériser la diversité des peuplements. D’aucuns parleraient de biodiversité, mais ce terme n’est pas tout à fait approprié ici. Lorsque l’écologue étudie les peuplements d’un écosystème, il va plutôt se référer à différents indices plus précis. Les premiers d’entre-eux concernent la richesse spécifique S, la biomasse B ou encore l’abondance A d’une espèce. Les seconds concernent la diversité spécifique à un habitat, voire un écosystème particulier.
La diversité spécifique prend ainsi en compte aussi bien le nombre d’espèces que la distribution des individus au sein de ces espèces. L’écologue tient ainsi à sa disposition plusieurs indices de diversité. Ceux-ci sont le plus souvent accompagnés d’indices d’équitabilité, qui traduisent la répartition des abondances d’espèces dans le peuplement. Grâce à ces indices, il devient possible de suivre l’évolution des peuplements au cours du temps, mais également de les comparer entre stations étudiées.

1. Indice de Shannon-Weaver
L’indice de diversité le plus couramment employé est l’indice de Shannon. Il est aussi appelé indice de Shannon-Wiener, bien que ces deux mathématiciens n’aient pas travaillé conjointement dessus. Historiquement, Claude Shannon était un mathématicien cryptographe qui cherchait à décrire l’entropie de caractères dans un texte (entropie de Shannon). Sa formule prend en compte la probabilité de rencontrer un caractère précis compris dans un ensemble de caractères utilisés. En écologie, le caractère est remplacé par une espèce présente et le texte étudié par le peuplement.
1.1. Formulation
H’ correspond à l’indice de Shannon, selon la formulation suivante :
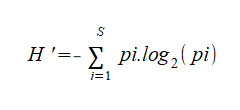
pi = l’abondance proportionnelle ou pourcentage d’abondance d’une espèce présente (pi = ni/N).
ni = le nombre d’individus dénombrés pour une espèce présente.
N = le nombre total d’individus dénombrés, toute espèce confondue.
S = le nombre total ou cardinal de la liste d’espèces présentes.
L’indice de Shannon permet d’exprimer la diversité spécifique d’un peuplement étudié. Pour rappel, la diversité spécifique caractérise le nombre plus ou moins grand d’espèces présentes dans un peuplement. S’il est homogène (constitué d’une seule et même espèce), alors l’indice H’ = 0.
Plus nous sommes en présence d’espèces différentes, plus sa valeur augmente de façon logarithmique. Il est ainsi fréquent de voir des valeurs H’ comprises entre 1 et 5 pour tenir compte de la diversité spécifique. Ceci est lié au fait que l’indice de Shannon est forcément lié à la taille de l’échantillon. Mais la comparaison de ces valeurs nécessite quelque prudence. Enfin, la valeur Hmax = log2(S) correspond à un peuplement hétérogène pour lequel tous les individus de toutes les espèces sont répartis d’une façon égale. L’indice H’ varie donc entre ces deux limites.
1.2. Indice d’équitabilité de Piélou
Pour mieux discuter cet indice de Shannon, il s’accompagne souvent de l’indice d’équitabilité de Piélou (J), ou indice d’équirépartition (E). Sa formule correspond au rapport entre H’ et Hmax : E = H’/Hmax. Cet indice varie donc entre 0 et 1. S’il tend vers E = 1, alors les espèces présentes dans le peuplement ont des abondances identiques. S’il tend vers E = 0, alors nous sommes en présence d’un déséquilibre où une seule espèce domine tout le peuplement.
Ces deux indices permettent notamment de suivre les changements temporels d’un peuplement (c’est-à-dire l’ensemble des espèces d’un territoire donné partageant une écologie semblable). L’apparition d’une espèce invasive ou les pics d’opportunistes entraînent une baisse significative conjointe de H’ et E. A l’inverse, un écotone (zone de transition écologique entre deux écosystèmes) ou un peuplement à l’équilibre présente des indices élevés. C’est pourquoi il faut prendre en compte ces deux indices de manière concomitante afin d’apprécier l’état d’un écosystème.
1.3. Discussion
Enfin, cet indice n’est pas insensible à la richesse spécifique (mesure de la biodiversité de tout ou partie d’un écosystème). En effet, la richesse spécifique se traduit par la valeur de S. Aussi l’indice de Shannon tend à augmenter lorsque sont présentes des espèces rares. Par exemple, le calcul de l’indice de Shannon sur un hotspot d’oiseaux migrateur réputé pour ses coches insolites en automne peut gonfler artificiellement avec le passage de raretés. De même, l’indice de Shannon est fortement dépendant du type d’habitat.
Les valeurs obtenues par l’indice de Shannon restent donc relatives, seulement comparables entre-elles pour des stations de mêmes peuplements ou selon une échelle temporelle. Employer cet indice comme valeur comparative absolue pour évaluer la qualité d’écosystèmes entre-eux présente donc un risque de confusion.
2. Indice de Simpson
Cet indice proposé par le statisticien Edward H. Simpson mesure la probabilité que deux individus pris au hasard appartiennent au même groupe. Ce brillant mathématicien est également célèbre pour son fameux paradoxe de Simpson (exemple statistique bien connu d’élèves d’autant plus brillants en sport qu’ils ont de mauvais résultats scolaires).
2.1. Formulation
Appliqué à l’écologie, l’indice de Simpson est la probabilité que deux individus sélectionnés au hasard appartiennent à la même espèce dans un peuplement. Plusieurs formes de l’indice existent dans la littérature scientifique, ce qui peut compliquer l’interprétation des valeurs.
Dans cet article, nous nous appuierons sur la probabilité que deux individus appartiennent à la même espèce selon la formule originelle de Simpson (1949) : P(ω) = Σ(pi²). Il en découle deux formules, suivant que l’échantillon est infini (tirage avec remises, indice λ) ou fini (tirage sans remises, indice L). Par exemple, dans le cas d’un peuplement de phytoplancton par m3 d’eau de mer, on préférera l’indice λ . Pour suivre une population d’oiseaux forestiers par hectare, nous utiliserons l’indice L.
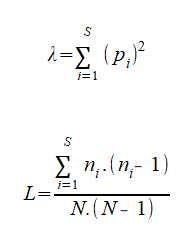
pi = proportion d’individus de l’espèce i (pi = ni/N).
ni = nombre d’individus de l’espèce i
N = nombre total d’individus.
S = le nombre total ou cardinal de la liste d’espèces présentes.
Plus cet indice est proche de 1, plus le peuplement est homogène. Aussi utilise-t-on fréquemment un second indice, ou indice de diversité, correspondant à l’indice de Simpson retranché à 1.
2.2. Indice de diversité
Cet indice de diversité est tout d’abord plus intuitif de lecture que l’indice de Simpson. Sa formule correspond à D = 1- λ ou D = 1 – L (selon la taille de l’échantillon étudié). Lorsque D = 0 , alors une seule espèce est présente dans le peuplement. Si toutes les espèces ont la même probabilité pi = 1/S de présence, alors D = 1-(1/S). Enfin, la valeur D = 1 apparaîtrait dans le cas de figure où un nombre infini d’espèces sont présentes, mais toutes de probabilité quasi-nulle.
2.3. Indice d’équitabilité
Il s’accompagne d’un indice d’équitabilité ED = D/Dmax . Pour Hurlbert, le cas où toutes les espèces sont présentes selon la même probabilité correspond au maximum de l’indice de diversité, soit Dmax = 1-(1/S).
Un autre formulation de l’indice de Simpson stipule que D = 1/λ (indice de diversité statistique). Il devient ainsi possible de considérer que si ED = D/Dmax alors Dmax = S. Soit l’équation ED = D/S. Le choix de la formule est donc crucial pour comparer les résultats entre-eux.
L’indice d’équitabilité de Simpson permet de traduire la dominance d’une espèce (ED tend vers 0) ou la codominance de plusieurs espèces (ED tend vers 1). Comme précédemment, il est prudent d’examiner plusieurs indices.
2.4. Discussion
L’indice de diversité de Simpson donne plus de poids aux espèces abondantes qu’aux espèces rares. La présence d’espèces rares dans le peuplement ne modifie pratiquement pas la valeur de l’indice de diversité, contrairement à l’indice de Shannon beaucoup plus sensible. C’est pourquoi il se prête mieux à des comparaisons entre habitats ou écosystèmes donnés.
Indice de Hill
Cet indice propose une mesure de l’abondance proportionnelle, en comparant entre-eux les indices de Shannon et de Simpson. L’indice de diversité de Hill ainsi obtenu a pour objectif d’apprécier le rapport entre d’un côté la prise en compte des espèces abondantes (Simpson) et de l’autre l’influence des espèces rares (Shannon). L’indice de Hill apparaît donc comme un indice synthétique.
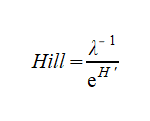
Lorsque Hill tend vers 0, alors la biodiversité est plus importante. Il est également possible de convertir cette valeur en (1 – Hill) afin que l’indice soit croissant avec la biodiversité présente. Cet indice peut sembler plus pertinent dans une synthèse de résultats terrain, cependant il peut être intéressant de comparer les trois indices simultanément pour mieux apprécier la structure des communautés.





