Les intervalles de confiance ne se limitent pas qu’aux petites lignes des sondages publiés dans la presse. Ils sont aussi la botte secrète des scientifiques. Là où les variables aléatoires continues font régner l’incertitude de la mesure expérimentale, elles redonnent une confiance (estimée) à nos résultats. « In God we Trust, all others bring data » disait le statisticien William Edwards Deming.
Mais pour autant, il ne faudrait pas tomber dans le piège d’une croyance aveugle dans les intervalles de confiance. Il n’est pas l’intervalle mathématique dans lequel se trouve obligatoirement prédit votre résultat expérimental. En effet, l’intervalle de confiance s’accompagne d’une probabilité. Ainsi pouvons-nous argumenter que si la variable aléatoire continue peut prendre une infinité de valeurs, le tirage place notre valeur très probablement (avec un seuil de confiance %(p) ) dans cet intervalle de confiance.

6. Estimations et intervalles de confiance
Pour une variable aléatoire suivie à partir d’un échantillon n, nous souhaitons connaître une estimation des paramètres de la population N. Il peut s’agir d’une méthode de sondages, d’une étude biométrique ou encore du suivi d’un caractère génétique dans une population.
6.1. Les estimations en statistiques
Supposons que nous ayons suivi une caractéristique précise d’un échantillon n de la population. Nous obtenons une variable aléatoire que nous pouvons associer à une loi de probabilité (loi binomiale, de Pascal, de Poisson, loi hypergéométrique, loi normale … ). Nos observations permettent de décrire les caractéristiques de l’échantillon. Mais désormais, nous souhaitons connaître les paramètres de la population entière.
Pour cela, il va nous falloir estimer le paramètre θ associé à la loi de probabilité choisie. Bien que nous ne disposions que d’un échantillon n de la population, nous allons définir une fonction particulière appelée estimateur. Cette fonction de notre variable aléatoire nous permet donc d’estimer certaines caractéristiques de la population totale.
Ces estimateurs sont donc au cœur de la statistique inférentielle. Pour estimer la qualité d’un estimateur vis à vis de son paramètre, nous pouvons examiner leur convergence, leur biais, ou encore leur robustesse.
6.1.1. Propriétés de l’estimateur
Nous associons d’abord un échantillon aléatoire n (x1+ x2+ x3+ … + xn) issu d’une variable aléatoire Xn à un des ses paramètres θ. Cela peut être son espérance E(Xn) , sa variance Var(Xn) ou encore sa moyenne X̅n .
Un estimateur ϑ du paramètre θ est une fonction qui dépend uniquement du n-échantillon (x1+ x2+ x3+ … + xn). Il est dit convergent s’il est « proche » de θ dans le sens où la valeur absolue|ϑ-θ| = ϵ et de sorte que la probabilité P(|ϑ-θ| > ϵ) = 0 lorsque n → ∞.
L’estimateur ϑ est donc fonction de Xn et peut s’écrire ϑ = f(Xn) .
Le biais ou erreur systématique correspond à l’espérance E(ϑ) de l’estimateur retranchée de son paramètre θ : biais(ϑ) = E(ϑ) – θ . L’estimateur est dit sans biais si E(ϑ) = θ lorsque n → ∞ (et alors E(ϑ)-θ = 0).
6.1.2. Erreur quadratique moyenne
L’erreur quadratique moyenne EQM est une mesure de la « précision » de cet estimateur. Elle se formule selon l’équation EQM = E[(ϑ-θ)²] . Nous pouvons déduire de la formule du biais vue précédemment que le paramètre θ = E(ϑ) – biais(ϑ) . Soit EQM = E[(ϑ – E(ϑ) + biais(ϑ))²] . Si nous développons cette formule, nous obtenons EQM = biais(ϑ)² + Var(ϑ) soit EQM la somme du biais de l’estimateur au carré et de sa variance.
Cette seconde formulation nous indique que pour choisir l’ECM la plus petite possible, il faut alors que l’estimateur ϑ soit sans biais et que sa variance soit faible. La variance étant toujours positive ou nulle, nous pouvons aussi noter que ECM ≥ 0. Nous choisirons donc, parmi les estimateurs convergents et sans biais, celui de plus petite variance.
En d’autres termes, il faut que l’estimateur ne varie pas trop autour de sa moyenne pour être efficace.
6.1.3. Robustesse statistique
En statistiques, la robustesse d’un estimateur est un qualificatif indiquant qu’une modification des données ou une valeur aberrante ne vient pas perturber outre mesure le modèle choisi.
Par exemple, la moyenne n’est pas un estimateur robuste car elle est affectée par des données aberrantes. A l’inverse de la médiane, beaucoup plus tolérante en cas d’énormités. Souvenez-vous de la petite phrase suivante : « en statistiques, la sardine du port de Marseille affole la moyenne, mais pas la médiane » .

6.2. Estimation ponctuelle
Nous avons déjà vu dans le chapitre 3 les formules d’espérance et de variance pour des variables aléatoires. Il s’agit dans cette section de déterminer deux catégories d’estimations ponctuelles : la moyenne et la variance.
Nous supposons ici un tirage aléatoire de n individus dans une population N. A partir d’un caractère quantitatif Y que nous décrivons comme variable aléatoire, qui dans la population est de moyenne Ȳ et de variance Var(Y). Au sein de l’échantillon de n observations (y1+ y2+ y3+ … + yn), la moyenne du caractère y dans l’échantillon se note ȳ et sa variance σ² .
6.2.1. Estimation d’une moyenne
Soit un échantillon de n observations (y1+ y2+ y3+ … + yn) . La moyenne ȳ des variables aléatoires associées est alors :

La moyenne observée est un estimateur convergent et sans biais car en effet E(X̅n) = µ lorsque n → ∞ . De surcroît, elle est donc aussi un estimateur efficace de l’espérance mathématique µ , soit ϑ(µ) = ȳ .
6.2.2. Estimation d’une variance
La formule classique de la variance σ² est donnée comme la moyenne des carrés des écarts à la moyenne. Sa formule pour notre exemple traité est bien connue :

Attention cependant, cette formule n’est pas une estimation ! Nous définissons ici la variance observée (ou variance empirique) s² . Pourquoi changer de formule ? Malheureusement parce que la variance σ² est biaisée, ce qui signifie que lorsque n tend vers l’infini, l’espérance de cet estimateur ne tend pas vers son paramètre.
Pour obtenir une bonne estimation de la variance d’un caractère dans un échantillon, il faut multiplier σ² par n/(n-1) soit σ².n/(n-1) = s² . Pourquoi cette transformation ? Car le calcul de la variance suppose que nous connaissions exactement la moyenne à n échantillons. Soit en d’autres termes l’espérance µ. Or nous venons d’estimer cette espérance : ϑ(µ) = ȳ .
Nous formulons donc un calcul de variance s² non pas avec la moyenne des carrés des écarts à µ mais à ȳ. En effectuant un calcul de correction de la variable aléatoire Var(Y), nous obtenons alors un facteur (n-1).σ²/n , ce qui signifie clairement que l’espérance de cet estimateur ne tendra pas vers σ² ! Il est donc biaisé d’une valeur (n-1)/n et il faut le débiaiser en multipliant σ² par n/(n-1). Soit in fine la formulation de l’estimateur s² de la variance sans biais :

6.3. Estimations par Intervalles
Aussi précise que soit une estimation, elle ne peut jamais être exacte. Elle sera donc toujours une valeur approchée du paramètre estimé. Si nous voulons mesurer la qualité de l’estimation, nous pouvons utiliser les intervalles de confiance.
6.3.1. Principe général
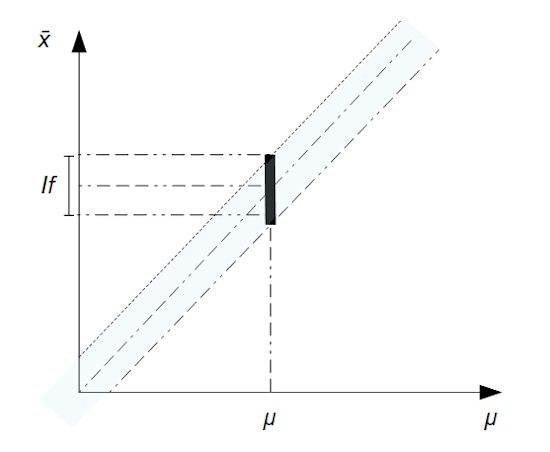
Soit une variable aléatoire X dans un échantillon n. L’estimateur de la moyenne est noté ϑ(µ) = x̄ . A partir d’un risque d’erreur α , nous allons déterminer un intervalle de fluctuation If de la moyenne observée x̄ au seuil de confiance (1 – α). Cet intervalle encadre la valeur µ.
Si nous avons recours à la variable aléatoire moyenne X̅, estimateur de l’espérance µ, alors cet intervalle est symétrique :
If (µ) = [µ – dα ; µ + dα]
On caractérise les bornes de cet intervalle par une probabilité :
P(X̅ < µ – dα) = α/2 , soit P(µ – dα ≤ X̅ ≤ µ + dα) = 1 – α et P(X̅ > µ – dα) = α/2
L’ensemble des intervalles de fluctuation pour chaque espérance µ crée une zone graphique appelée domaine de fluctuation. A l’inverse, si nous souhaitons connaître l’intervalle de confiance Ic(x̄) encadrant une valeur x̄ de la moyenne observée au seuil de confiance (1 – α), il suffit d’inverser la méthode.
6.3.2. Intervalles de confiance de moyennes de grands échantillons
Soit une variable aléatoire X pour un échantillon n ≥ 30 de la population suivant une distribution de loi normale N(µ ; σ²). La moyenne X̅ calculée sur cet échantillon suivra elle aussi une loi normale N(µ ; σ²/n). En effet, nous nous attendons à ce que X̅ ≈ µ lorsque nous généralisons les résultats obtenus sur l’échantillon à l’ensemble de la population.
Cependant, nous avons là une approximation. La formule plus exacte serait de considérer que X̅ = µ ± ϵ (soit ϵ la marge d’erreur). Nous allons donc chercher à déterminer cette marge d’erreur.
L’échantillon n ≥ 30 est grand, il suit donc une loi normale et nous pouvons appliquer le théorème central limite. Nous pouvons remplacer σ² par l’estimateur de la variance s² calculé sur l’échantillon pour décrire la loi normale s’appliquant à X̅ ∼ N(µ ; s²/n) . Cette distribution est centrée à µX̅ = µ et a pour erreur standard σX̅ = √(s²/n).
Il nous faut ensuite associer la côte Zi associée au niveau de confiance 1 – α à la moyenne. Cette valeur est donnée par les tables de loi normale. Par exemple, pour 95% de confiance, 1 – α = 0,95 et α/2 = 2,5 % = 0,025. Soit dans les tables de loi normale P(Z ≤ Zi) = 0,975 est vérifiée pour Zi = 1,96.
Nous en déduisons l’intervalle de confiance pour cette moyenne en suivant la formule :
µ = X̅ ± Zi.σX̅ = X̅ ± Zi.√(s²/n)
Par exemple, la moyenne de taille observée dans une classe de 45 étudiants est de 183,45 cm. La variance estimée vaut s² = 50,384. Calculons l’écart à la moyenne à 95 %.
L’erreur standard vaut √(s²/n) = √(50,384/40) = 1,122 cm. Pour 95% de confiance, 1 – α = 0,95 et Zi = 1,96. La limite inférieure de mon IC = 183,45 – 1,96.1,122 = 181,25 cm ; la limite supérieure de mon IC = 183,45 + 1,96.1,122 = 185,65 cm. Soit IC = [181,25 ; 185,65] à 95 % de confiance.

6.3.3. Intervalles de confiance de moyennes de petits échantillons
Dans ce cas de figure, la variance s² calculée à partir d’un petit échantillon donne une approximation trop grossière de la variance σ² pour la population. Il y a donc un risque de sous-estimer σ² si l’on utilise la relation X̅ = N(µ ; σ²/n) .
Pour éviter de tomber dans ce piège, nous allons avoir recours à la variable centrée-réduite t de Student pour définir l’intervalle de confiance :


Les variables t sont elles aussi indiquées dans la table de Student, un tableau à double entrée. Pour lire la valeur t, il nous faut prendre en compte le risque d’erreur α (ou α/2 , ou le niveau de confiance 1 – α ; selon la table), ainsi que le degré de liberté (ddl). Pour calculer le degré de liberté, il suffit de retrancher (n – 1) au nombre de variables aléatoires de l’échantillon. Comme nous l’avons vu dans le chapitre 4, l’échantillon n équivaut à autant de variables aléatoires répétées. Donc pour un échantillon n = 12 , ddl = n – 1 = 12 – 1 = 11.
Par exemple, on dose les protéines dans quatre échantillons pris au hasard dans le stock de lait d’une laiterie. X̅=30 g/l et S2= 16 (g/l)2 . Calculer l’IC à 95%.
Reprenons les données : s = 4 g/l, n = 4, le ddl = 3 et α = 1 – 0,95 = 0,05. Soit pour l’IC d’un petit échantillon t(3;0,05) = 3,182 . Soit ϵ = t.√(s²/n) = 3,182.(4/2) = 6,364 g/l. Ce qui nous donne IC95 = [23,64 ; 36,36] .
Quelle est la suite ? Dans l’épisode VII, nous assisterons au réveil de la régression linéaire. Ce chapitre introductif nous révélera que comme Monsieur Jourdain face à MS Excel, nous faisons de la régression linéaire depuis fort longtemps sans le savoir !





