Logiciel R : un outil de Data Science pour les naturalistes

L’écologue comme le naturaliste collectent une multitude de données. Vient ensuite l’heure tant redoutée du traitement statistique de ces données. Aussi, le développement des data sciences s’avère un nouvel outil pertinent pour les sciences naturalistes. Cet article vous propose donc de découvrir un moyen informatique de traiter ses données statistique largement employé en biologie. L’incontournable outil ne se présente plus, il s’agit donc du logiciel libre R.

Cependant, pour quiconque ayant déjà employé le logiciel R, cet article ne présentera aucune nouveauté. En effet, il se destine avant tout aux naturalistes les plus hétérogènes aux statistiques. Ceux d’entre-vous qui angoissent à la vue d’un livre de maths et qui associent Matrix aux mots-clés big data, machine learning et informatique. Sachez tout d’abord que parler data science en naturalisme, ce n’est pas tabou ! Bien au contraire, des outils informatiques comme R ou RStudio ne peuvent que faire progresser notre compréhension de la Nature.

Dans cet article, vous trouverez donc un petit guide pratique du naturaliste perdu dans le royaume du langage R. En quelques sections pratiques, je vous invite à prendre en main cet outil pour réaliser quelques traitements simples. Pour paraphraser le célèbre statisticien John Tukey, le but des data sciences est de nous simplifier le travail ! Notez cependant que cet article ne se substitue en rien à un cours de statistiques. Les bases des biostatistiques sont exposées dans une série d’articles dédiés. Vous pouvez donc vous y référer si besoin. Pour le reste, il existe sur le web suffisamment de cours en ligne pour vous éclairer.

1. Prise en main du logiciel R

1.1. Introduction

D’abord, R est un puissant logiciel d’analyse et de traitement de données. Les tableurs comme MS Excel peuvent déjà faire beaucoup d’opérations, mais ils s’avèrent rapidement limités et certains utilisateurs sont rapidement frustrés par les limites de leurs représentations graphiques. Avec R, le champ des possibles est ainsi quasi-illimité ! Vous pouvez mettre en forme vos graphiques, effectuer des analyses statistiques, mais aussi créer des plans d’expérience, effectuer du traitement de signal, l’utiliser comme un util cartographique (SIG) ou encore analyser des images… Enfin R est un logiciel gratuit, disponible pour la plupart des OS (UNIX, Windows, MacOS). C’est pourquoi les chercheurs écologues l’utilisent depuis plusieurs années déjà, avec succès !

Quelques repères :

• R est un logiciel libre qui permet d’effectuer des graphiques et calculs mathématiques. Vous pouvez le télécharger via ce site miroir français.
• L’interface du logiciel R procède par langage de programmation R. Pour exécuter une commande, il faut la rédiger dans la console.
• Bien que le logiciel R propose de nombreuses fonctionnalités, vous pouvez en télécharger d’autres sous forme de packages (FactoMineR, ggplot2, …).
• RStudio une interface graphique qui facilite votre travail sous R. Vous pouvez utiliser RStudio ou une autre interface, ou bien exécuter directement R.

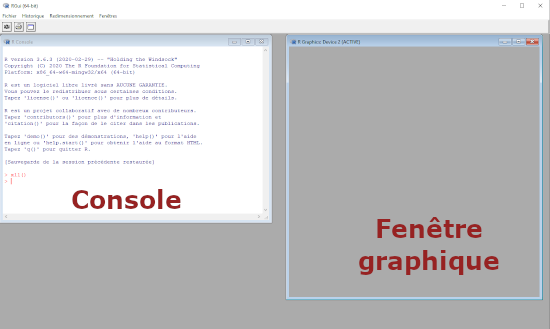
1.2. La console R

Une fois le logiciel R installé, lancez le programme. Vous obtenez une fenêtre avec un interface en lignes de commandes appelée console R. Par la suite, une autre fenêtre graphique s’affichera selon les fonctions exécutées.

1.2.1. Enregistrer et quitter sa session

Pour quitter le logiciel R, vous pouvez passer par le menu ou bien en tapant la ligne de commande q(). Cela vous permettra de relancer plus tard votre session au redémarrage du logiciel. Si vous ne voulez pas sauvegarder, il suffit de taper la commande :

q(save="no")

Il est préférable de sauvegarder dans un dossier spécifique. Vérifiez d’abord quel est le répertoire de sauvegarde par défaut :

getwd()

[1] "D:/D_Statistiques/sauvegarde"

Pour en changer, voici un exemple de commande setwd() qui définit un dossier précis. La commande dir() lit le contenu du répertoire courant.

setwd('D:/D_Statistiques/sauvegarde') 

Enfin, pour sauvegarder l’historique des commandes récemment enregistrées ou sauvegarder une image de son travail (format .RData), il faut renseigner les deux commandes ci-dessous :

savehistory(file="test.Rhistory")

save.image("svg.RData")

1.3. Les packages

Ces collections de fonctions pré-programmées permettent de faciliter votre utilisation de R afin d’effectuer des tâches spécifiques. Il peut s’agir de packages graphiques, statistiques, cartographiques, etc… La liste des packages disponibles est en effet très longue ! Certains d’entre-eux sont déjà installés sur la version basique de R. Pour cela, allez dans le menu Packages > Charger le package pour dérouler la liste. Vous pouvez ainsi cliquer sur le package à activer, bien entendu nous aurons occasion de citer quelques exemples.

Si un package n’est pas disponible sur votre version de R, il suffit d’aller dans le menu Packages > Installer le(s) package(s) . S’il s’agit de votre premier ajout de package, le logiciel vous demandera de choisir un site miroir pour le téléchargement. Je vous conseille d’utiliser un site français, mais aucune obligation. Sélectionnez ensuite le package qui vous intéresse et lancez l’installation. La console R vous indiquera lorsque l’opération sera achevée.

Nous avons vu comment installer et charger un package sous R. Notez cependant que vous pouvez lancer ces commandes directement sans passer par le menu. La commande library() charge automatiquement un package. Si vous avez besoin d’afficher de l’aide pour une fonction, tapez le signe ? avant la fonction. Par exemple, ?attach donne ainsi la fenêtre d’aide en ligne de la fonction attach().

1.4. Programmation basique

1.4.1. Opérateurs basiques

Prenons quelques exemples d’opérations basiques. Tapez 2+2 dans la console et appuyez sur la touche « entrée ». Vous obtenez la ligne [1] 4. Le logiciel indique que la seule réponse disponible [1] est la valeur « 4 ». Notez que vous pouvez rajouter des espaces sans que cela ne change l’interprétation de la ligne de commande. Voici enfin d’autres exemples :

1+1

[1] 2

2+2

[1] 4

1/3

[1] 0.3333333

4+52 

[1] 14 

3/6(5+6+5)

[1] 8

1.4.2. Les objets sous R

Sous R, il est important de créer des objets. En effet, cela permet de mémoriser des opérations ou les résultats de fonctions. Il suffit ensuite de taper le nom de l’objet pour afficher son contenu.

Les objets peuvent être des valeurs ou de commandes spécifiques. Pour renseigner un objet, il faut d’abord taper son nom puis lui associer une information avec les symboles « <- » ou « = ». Par exemple, x <- 12 permet de renvoyer la valeur 12 en exécutant x sur la console.

x <- 12

x

[1] 12

1.4.3. Les fonctions sous R

Nous avons déjà vu quelques fonctions sous R, il s’agit en effet des commandes s’achevant avec () sans espaces. Par exemple la fonction citation() renvoie les références bibliographiques de R. De plus, il est possible de créer des objets contenant des fonctions. Cela permet d’exécuter et de sauvegarder le résultat de la fonction.

Pour concaténer des valeurs de même type en un seul objet appelé vecteur sous R, il faut par exemple utiliser la fonction c() :

vecteur <- c(1,2,3,4,5,6,7,8,9,10)

vecteur

[1] 1 2 3 4 5 6 7 8 9 10

Un vecteur est une liste d’éléments du même type (numériques, caractères, logiques). C’est un objet idéal pour constituer une variable aléatoire.

y <- c("Pouillot","Aigle","Busard","Bouvreuil")

z <- c(TRUE,FALSE,TRUE,FALSE)

Il est également possible de constituer de lister des variables d’attributs et de tailles différentes grâce à la fonction list() :

x1 <- c(1,2,3,4)

x2 <- c("a","b","c")

x3 <- 3

x4 <- matrix(nrow=2,ncol=2)

liste <- list(x1=x1,x2=x2,x3=x3,x4=x4)

Pour rajouter un commentaire, il suffit de débuter la ligne avec le symbole # qui indiquera qu’il ne s’agit pas de code exécutable. Par la suite, d’autres fonctions permettent d’effectuer des calculs statistiques. Ici, la fonction mean() :

#La moyenne de 3 valeurs :

mean(c(1,2,3))

[1] 2

#La moyenne des valeurs du vecteur :

mean(vecteur)

[1] 5.5

Quelques autres fonctions courantes :

#L'écart-type de l'objet vecteur :

sd(vecteur)

[1] 3.02765

#Opérateurs mathématiques divers :

sqrt(16)

[1] 4

log10(6.1)

[1] 0.7853298

exp(3.14)

[1] 23.10387

1.4.4. Simuler des données sous R

Supprimons maintenant l’objet x pour en créer un nouveau. J’utilise alors la fonction rm() puis je vérifie que l’objet est bien supprimé. Ensuite, je décide de créer un vecteur de valeurs :

rm(x)

x

Erreur : objet 'x' introuvable

x <- 1:10

x

[1] 1 2 3 4 5 6 7 8 9 10

x <- sample(x)

x

[1] 8 6 1 5 7 3 4 10 9 2

Nous voulons créer un vecteur de 100 valeurs suivant la loi normale, moyenne 20, écart-type 3. La fonction rnorm() va nous permettre de simuler ces données. Notez que le logiciel R renvoie entre crochets des repères de lecture en dénombrant les réponses obtenues.

x <- rnorm(100,20,3)

x

[1] 18.10743 12.18692 18.60615 20.54304 15.16833 15.12411 17.80325 17.78761

[9] 18.61578 21.07069 21.64065 17.72874 20.99421 19.39959 20.14687 20.47614

[17] 23.66195 18.30205 23.01821 19.35469 21.84486 24.36155 15.10932 17.46974

[25] 24.88512 20.48678 19.15544 23.02902 22.34409 18.91447 22.86923 13.87309

[33] 17.44306 24.72212 19.08051 19.91710 21.45763 18.30780 21.72041 20.18708

[41] 19.11926 20.41482 21.19013 21.83345 21.43669 20.69209 18.05678 17.14987

[49] 14.74178 25.09662 20.00481 21.17985 25.78722 18.19263 16.89537 19.03157

[57] 20.30773 18.75206 21.05013 22.48717 21.10322 17.27790 23.89495 19.57024

[65] 18.62064 24.48664 20.24659 22.45937 21.84860 12.42304 24.54611 22.74259

[73] 17.96815 20.97834 16.90642 19.32163 23.75901 21.14499 22.14897 21.26138

[81] 18.41145 18.23158 19.69066 19.08212 23.97170 19.91118 20.76197 18.96378

[89] 22.36301 20.92960 18.90683 21.12082 19.33202 20.24820 19.31803 18.26171

[97] 21.23974 19.40294 25.04944 24.23378

2. Représentations graphiques

2.1. Tracer un graphique avec le logiciel R

2.1.1. La fonction plot()

Pour tracer un graphique à partir d’une fonction mathématique y = f(x), l’une des méthodes les plus simples consiste à utiliser la fonction plot(x,y). Par exemple, pour générer un graphique aléatoire de 100 points sans aucune donnée, testez ce script :

x <- 1:100

x <- sample(x)

y <- 1:100

y <- sample(y)

plot(x,y)

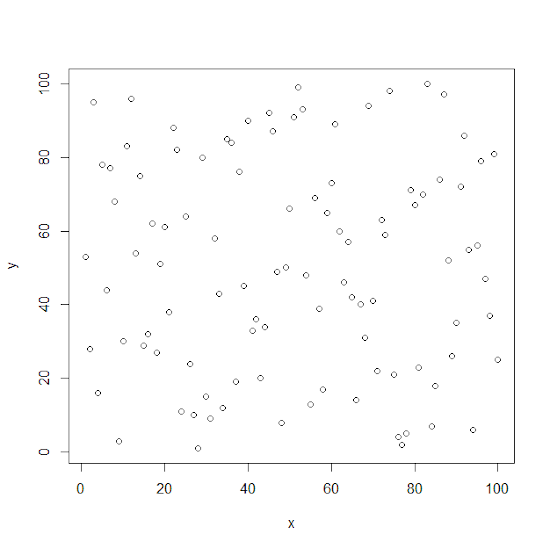
Ce n’est pas très joli mais nous avons affiché un graphique dans la bonne fenêtre. Si vous relancez une autre fonction plot() le nouveau graphique écrasera le précédent. Si vous voulez ouvrir une autre fenêtre graphique, utilisez alors la fonction x11() et tapez sur « entrée ».

2.1.2. Mise en forme des graphiques

Voici un petit exemple d’amélioration de la mise en forme d’un graphique. Nous relançons un nouveau script ci-dessous :

x <- 1:160

x <- sample(x)

y <- 1:160

y <- sample(y)

plot(x,y,pch=17,col="red",main="Graphique aléatoire",xlab="Hasard",ylab="Chance")

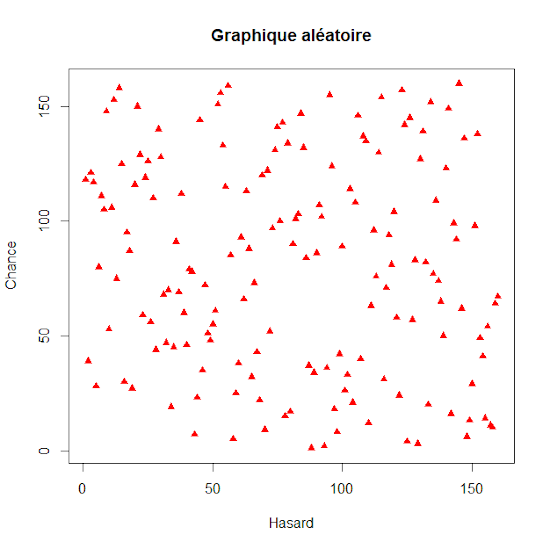
Dans la fonction plot() apparaissent de nouveaux attributs. Le type de points se modifie avec pch=17 (le numéro permet de charger un motif pré-enregistré sous R). La couleur des points est rouge grâce à col= »red ». Le titre du graphique se renseigne avec l’attribut main. Enfin, xlab et ylab permettent de nommer les axes du graphique.

Pour en savoir plus sur la mise en forme basique des graphiques, je vous conseille ce cours en ligne. Notez également que pour améliorer l’esthétique de vos oeuvres, vous pouvez recourir à des packages comme ggplot !

2.2. Types de graphiques sous R

La fonction plot() permet de générer des nuages de points. Mais fort heureusement, il ne s’agit pas de la seule fonction graphique sous R. En voici un petit aperçu :

2.2.1. Diagramme en barres

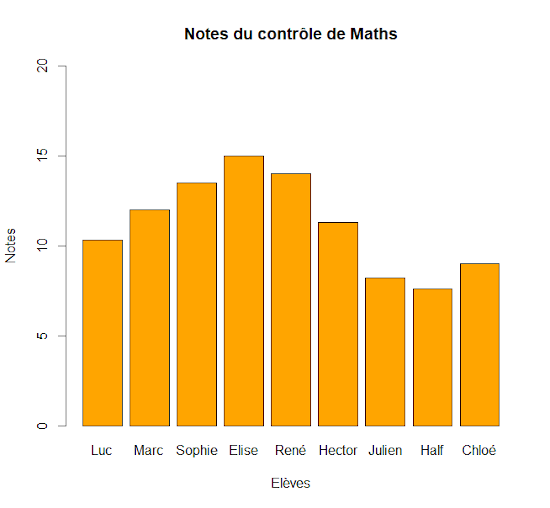
Pour effectuer un diagramme en barres, il est possible d’utiliser la fonction barplot(). Dans l’exemple ci-dessous, l’axe des abscisses renseigne le nom des barres grâce à l’attribut names.arg. Pour ce faire, nous l’avons relié à l’objet « eleves » défini précédemment.

notes <- c(10.3,12,13.5,15,14,11.3,8.2,7.6,9)

eleves <- c("Luc","Marc","Sophie","Elise","René","Hector","Julien","Half","Chloé")

barplot(notes,col="orange",names.arg=eleves,ylim=c(0,20),

    main="Notes du contrôle de Maths",xlab="Elèves",ylab="Notes")

2.2.2. Histogramme

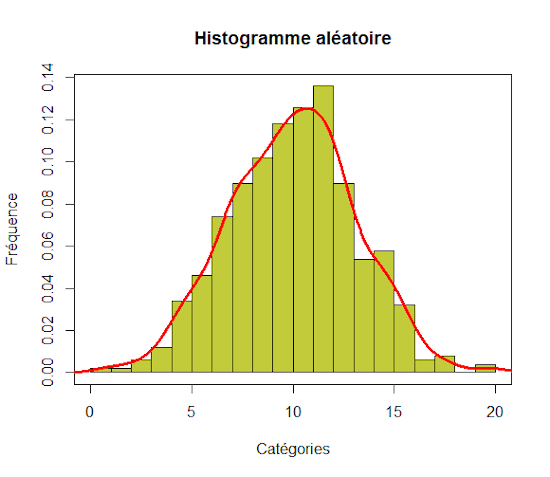
Un exemple d’histogramme aléatoire obtenu à partir de données simulées selon une loi normale N(10,3).

x <- abs(rnorm(500,10,3))

Nous utilisons la fonction hist() pour générer un histogramme, que nous fixons à breaks=15 colonnes. Par défaut, l’axe des ordonnées gradue selon le nombre de valeurs par colonne. Nous forçons la graduation de l’axe selon la fréquence des valeurs comprises par colonne freq=FALSE. Enfin, la fonction box() encadre le graphique.

hist(x,breaks=15,col="#c2cc3b",main="Histogramme aléatoire",

    ylab="Fréquence",xlab="Catégories", freq=FALSE)

box()

L’intérêt de cette graduation de l’axe des ordonnées par la fréquence est aussi que nous pouvons rajouter une courbe de densité. Il faut préalablement calculer la densité des valeurs, puis tracer la courbe avec la fonction line() dont l’attribut lwd permet de choisir l’épaisseur du trait.

densite <- density(x)

lines(densite, col = "red",lwd=3)

Nous obtenons le graphique ci-dessous :

2.2.3. Boîte à moustaches

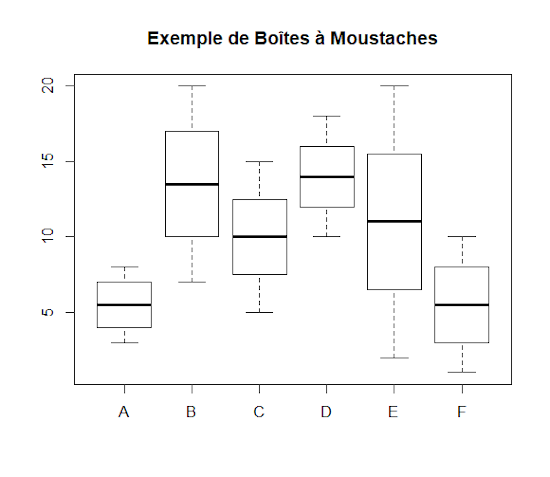
Cette représentation graphique est encore populaire en statistiques descriptives. Elle est régie par la fonction boxplot() dont voici un exemple :

a <- sample(3:8)

b <- sample(7:20)

c <- sample(5:15)

d <- sample(10:18)

e <- sample(2:20)

f <- sample(1:10)

boxplot(a,b,c,d,e,f,names=c("A","B","C","D","E","F"),

    main="Exemple de Boîtes à Moustaches")

2.2.4. Courbes et régressions linéaires

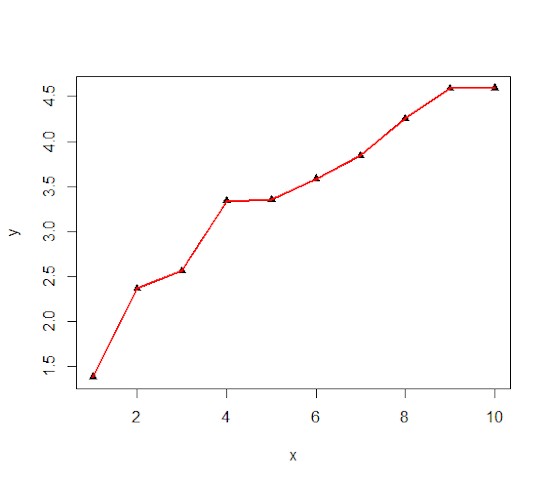
Nous avons déjà vu comment relier des points entre-eux avec la fonction line(). En revoici un rapide exemple, avec deux jeux de données pour générer les coordonnées x,y de chaque point. Notez que l’attribution des valeurs de la fonction lines() s’écrit de manière inversée y~x :

x <- c(1:10) ; y <- sort(rnorm(10,3))

plot(x,y,pch=17)

lines(y~x,col="red",lwd=2)

Enfin, abordons rapidement le tracé de droites de régression. Nous traçons tout d’abord le nuage de points du nombre de moutons en fonction de la superficie de prairies (données agricoles de l’UE).

plot(Meadows,Sheeps,col="#008b45",pch=13,

    ylab="Moutons",xlab="Superficie en prairies",


    main="Relation entre prairies et nombre de moutons")

La droite de régression se trace à partir de la fonction abline(b,a) qui permet d’obtenir des droites graphiques d’équation y =ax+b . Elle utilise pour le coefficient a une formule de régression linéaire passant par l’origine. Le résultat final est figuré ci-dessous.

abline(0,(lm(Sheeps~Meadows+0)$coefficients), col="black",lwd=2)

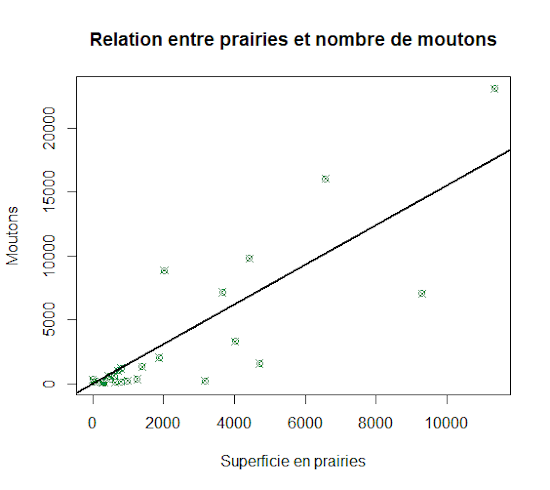
A noter que le logiciel R permet de fournir de nombreux outils pour les régressions linéaires. Un petit exemple, pour obtenir un résumé des informations statistiques de la régression linéaire ci-dessus, voici une technique rapide. Tout d’abord, créer une objet que nous nommons ici regress1. Puis utiliser la fonction summary() :

regress1 <- lm(Sheeps~Meadows)
summary(regress1)


Call:
lm(formula = Sheeps ~ Meadows)


Residuals:

Min 1Q Median 3Q Max

-7658.3 -658.3 109.4 609.9 6043.1



Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -495.0527 822.1042 -0.602 0.553

Meadows 1.6356 0.2181 7.499 1.28e-07 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


Residual standard error: 3165 on 23 degrees of freedom

Multiple R-squared: 0.7097, Adjusted R-squared: 0.6971

F-statistic: 56.23 on 1 and 23 DF, p-value: 1.278e-07

3. Analyses statistiques

3.1. Statistiques descriptives en langage R

Bien entendu, le logiciel R permet de programmer des analyses statistiques de vos données ! Pour commencer, voyons quelques formules pratiques en statistiques descriptives.

Fonction	Formule	Fonction	Formule
Moyenne	mean(x)	Minimum	min(x)
Médiane	median(x)	Maximum	max(x)
Variance	var(x)	Min + Max	range(x)
Ecart-type	sd(x)	Résumé statistique	summary(x)

3.2. Tests statistiques classiques

Parmi les nombreux tests statistiques possibles, nous prendrons deux exemples très classiques mais qui ne demandent pas d’explications statistiques trop poussées. Ils sont là uniquement pour vous montrer qu’il est très facile d’effectuer des tests statistiques sous R.

3.2.1. Test de Student

Grand classique des tests d’hypothèse, les tests de Student permettent de comparer des moyennes d’échantillon entre-elles ou de les confronter à une valeur théorique. La fonction utilisée sous R est t.test(x,y) avec deux attributs à renseigner. Il peut s’agir de deux objets de valeurs ou d’un objet et d’une moyenne mu= à renseigner. En voici deux exemples faits à partir du jeu de données « iris » disponible sur le logiciel R. Chargeons et décrivons tout d’abord le jeu de données :

data(iris)

attach(iris)

names(iris)

[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"

summary(iris)

Sepal.Length    Sepal.Width     Petal.Length     Petal.Width

Min. :4.300     Min. :2.000     Min. :1.000      Min. :0.100

1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600    1st Qu.:0.300

Median :5.800   Median :3.000   Median :4.350    Median :1.300

Mean :5.843     Mean :3.057     Mean :3.758      Mean :1.199

3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100    3rd Qu.:1.800

Max. :7.900     Max. :4.400     Max. :6.900      Max. :2.500

Species

setosa :50

versicolor:50

virginica :50

Nous nous proposons d’effectuer deux tests de Student : comparer les valeurs Sepal.Width à une moyenne théorique de 3.5 et comparer les moyennes de Petal.Width et Sepal.Width entre-elles :

t.test(Sepal.Width,mu=3.5)



#One Sample t-test



data: Sepal.Width

t = -12.439, df = 149, p-value < 2.2e-16

alternative hypothesis: true mean is not equal to 3.5

95 percent confidence interval:

2.987010 3.127656

sample estimates:

mean of x

3.057333

t.test(Petal.Width,Sepal.Width)



#Welch Two Sample t-test



data: Petal.Width and Sepal.Width

t = -25.916, df = 237.03, p-value < 2.2e-16

alternative hypothesis: true difference in means is not equal to 0

95 percent confidence interval:

-1.999237 -1.716763

sample estimates:

mean of x mean of y

1.199333 3.057333

Besoin d’aide pour comprendre l’interprétation par le p-value ? Je vous recommande alors le visionnage de ces deux vidéos fort instructives :

3.2.2. Tests du Khi-Deux

Le logiciel R permet d’effectuer aussi bien des tests χ² d’ajustement que d’indépendance. La fonction chisq.test() est à chaque fois la même, seule la mise en forme des données s’adapte aux deux tests.

Par exemple, pour un test d’ajustement entre deux caractères génétiques de forme de nageoire caudale chez des poissons. A et B; les fréquences alléliques sont %(A) = 30 % et %(B) = 70%. Sur un échantillon de 100 poissons prélevés, n(A) = 45 et n(B) = 55.

genetique <- c(0.3,0.7)

poissons <- c(45,55)

chisq.test(poissons,p=genetique)



#Chi-squared test for given probabilities



data: poissons

X-squared = 10.714, df = 1, p-value = 0.001063

Enfin, pour un test d’indépendance, il conviendra de rentrer son tableau de données sous forme d’une matrice avec la fonction matrix() comme dans l’exemple suivant comparant les tailles d’un échantillon d’hommes et de femmes :

hommes = c(184,191,175,195,200)

femmes = c(165,170,180,168,171)

table = matrix(c(hommes, femmes),2,5,byrow=T)

khi_test = chisq.test(table)

khi_test


#Pearson's Chi-squared test



data: table

X-squared = 2.0035, df = 4, p-value = 0.7351

3.2.3. Pour aller plus loin

Besoin d’effectuer encore plus de tests statistiques ? Je vous recommande quelques liens pertinents pour poursuivre votre lecture :

• Les analyses de variance ANOVA : tutoriel approfondi sur le blog de Claire Della Vedova.
• Les tests de normalité : une page web de l’Université de Brest.
• Regroupements de données (K-means, clustering) : l’excellent site d’Antoine Massé propose une initiation en ligne.

3.3. L’Analyse en Composantes Principales

L’ACP est un outil d’analyse à la fois géométrique et statistique. En effet, il représente les variables dans un nouvel espace et recherche un ou plusieurs axes indépendants pour lesquels les données sont les mieux dispersées (optimisation de la variance). L’ACP considère ainsi le premier de ces axes comme l’axe de première composante principale. Le second axe lui est ensuite perpendiculaire, il s’agit de la seconde composante principale. Nous avons donc au final deux axes, soit la définition d’un espace-plan.

L’analyse génère alors deux représentations graphiques 2D à partir de ces deux composantes principales. Il s’agit le plus souvent de graphiques orthonormés (à axes centrés). Une représentation des variables (cercle des corrélations) et une représentation des observations (graphique des observations).

Pour effectuer une ACP sous logiciel R, vous pouvez ainsi utiliser différents packages comme FactoMineR ou Factoshiny… Un article du blog aborde plus spécifiquement l’emploi de ces deux packages.

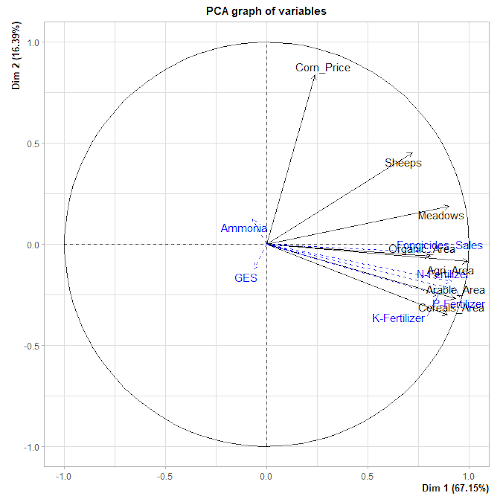
3.4. Intervalles de confiance

En travaux ! Section à venir.

4. Quelques packages pour logiciel R

Le logiciel R permet d’aller encore plus loin en écologie ! Dans ce dernier chapitre, je vous propose donc de découvrir quelques exemples d’applications avancées et une sélection de packages associés. Le but ici n’est pas de vous former en un temps record sur ces outils, mais de vous renseigner efficacement pour poursuivre votre exploration de R.

4.1. Améliorer la mise en forme graphique avec ggplot2

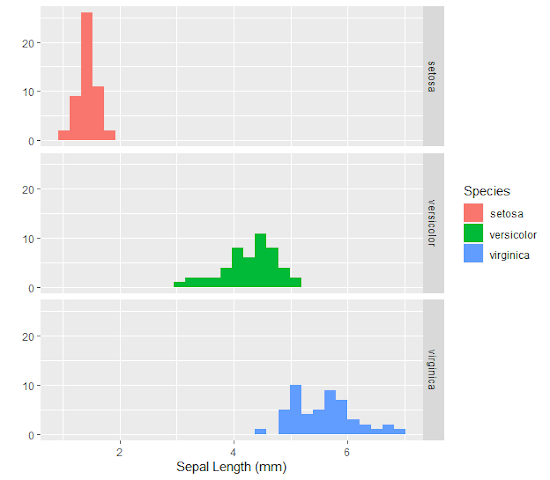
Incontournable de l’amélioration des graphiques sous R, le package ggplot2 permet d’approfondir la mise en valeur de vos données. Bien entendu, ce travail n’est pas seulement esthétique. Il se présente ainsi comme un outil d’exploration plus abouti des données sous forme graphique.

Le package ggplot2 est pré-installé sous R. Pour l’activer, il vous faut donc aller dans le menu Packages > Charger le package… Vous n’avez plus qu’à le sélectionner dans la fenêtre déroulante et cliquer sur OK. Pour vous donner une idée de l’intérêt des packages graphiques, voici une réalisation effectuée avec ggplot2 concernant les données « iris » . Notez comment les différences inter-espèces apparaissent clairement :

4.2. Analyse spatiale et SIG sous logiciel R

Bien que l’idée puisse sembler surprenante au premier abord, le logiciel R permet en effet de travailler sur de l’analyse spatiale ! Mais pour transformer R en un véritable SIG, il faut procéder à l’installation de packages bien spécifiques. Par exemple, le package OpenStreetMap qui permet d’accéder aux images Raster du serveur.

Dans un avenir proche, je vous proposerai aussi un article détaillé sur l’analyse spatiale sous logiciel R. Pour le moment, je vous en donne un aperçu avec un exemple de carte :

5. Remerciements et citations

citation()

R Core Team (2020). R: A language and environment for statistical

computing. R Foundation for Statistical Computing, Vienna, Austria.

URL https://www.R-project.org/.