L’analyse en composantes principales (ACP) est une méthode statistique d’analyse de données. Elle consiste à traiter plusieurs variables aléatoires quantitatives pour en récupérer de nouvelles informations. Ces variables sont contenues dans une matrice de donnée. Elles sont ensuite transformées en de nouvelles variables appelées composantes principales ou axes principaux. L’ACP permet ainsi de passer d’un nuage de points de k variables contenu dans un espace à k dimensions, à une représentation en deux dimensions.
Historiquement, l’ACP naît dans un article de Pearson, publié en 1901 dans la revue Philosophical Magazine. Elle est ainsi sous le nom de transformée de Hotelling ou transformée de Karhunen-Loève. Hotelling développera grâce à cela l’analyse canonique des corrélations, qui est une généralisation mathématique des analyses factorielles. De nos jours, l’ACP est un outil statistique incontournable en data science. Son usage se retrouve aussi bien en écologie qu’en recherche médicale, économie, marketing, sociologie, traitement d’images…
Bien que l’ACP ne concerne que des variables aléatoires quantitatives, d’autres outils similaires existent selon le type de variables. L’analyse des correspondances multiples (ACM) traite ainsi les variables qualitatives. Tandis que l’analyse factorielle multiple (AFM) utilise des variables mixtes.
1. Principe général
L’outil est à la fois géométrique et statistique. En effet, il représente les variables dans un nouvel espace et recherche un ou plusieurs axes indépendants pour lesquels les données sont les mieux dispersées (optimisation de la variance). L’ACP considère le premier de ces axes comme l’axe de première composante principale. Le second axe lui est perpendiculaire, il s’agit de la seconde composante principale. Nous avons au final deux axes, soit la définition d’un espace-plan.
L’ACP génère alors deux représentations graphiques 2D à partir de ces deux composantes principales. Il s’agit le plus souvent de graphiques orthonormés (à axes centrés). Une représentation des variables (cercle des corrélations) et une représentation des observations (graphique des observations). Les dimensions sont des facteurs ou axes. En ACP, l’information est appelée inertie. Il s’agit de la dispersion du nuage de points dans les k dimensions d’origine. Pour évaluer la quantité d’information conservée par la transformation ACP, on calcule pour chaque axe le pourcentage d’inertie. Plus la composante principale est forte, plus son pourcentage d’inertie est important.
2. Le cercle des corrélations
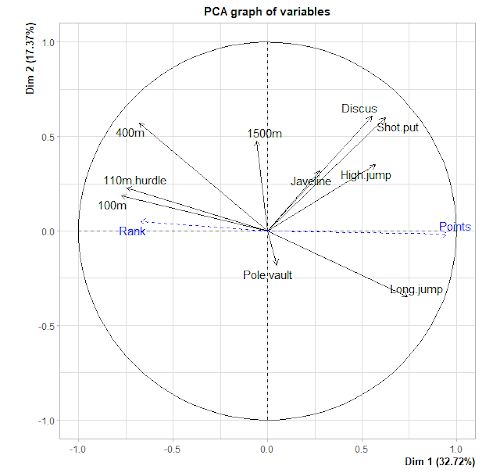
Chaque axe correspond à une composante principale. L’affichage des pourcentages d’inertie permet de d’indiquer la position de l’axe de première composante principale (généralement horizontal ou axe des abscisses). Chaque vecteur représente une variable.
- Deux vecteurs de variables forment un angle aigu ( < 90° ) : corrélation positive.
- Deux vecteurs de variables présentent un angle obtus ( > 90° ) : corrélation négative.
- Les vecteurs de variables définissent un angle droit (90°) : variables indépendantes.
Les tailles de vecteur informent sur la qualité de représentation des variables sur les axes retenus. Si le vecteur est court, alors l’information est moins bien représentée sur les axes de composante principale retenus.
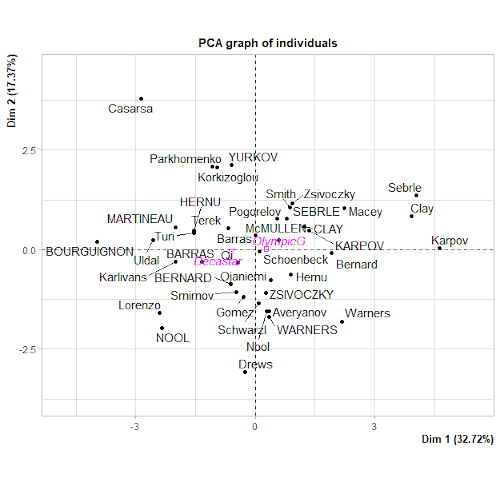
3. Le graphique des observations
Il permet d’évaluer les liens entre individus et variables. A nouveau, il s’agit d’un graphique à deux dimensions défini selon les axes de composante principale. L’axe premier est horizontal, l’axe second est vertical. Il permet de faire apparaître la dispersion des données par rapport aux vecteurs générés par le cercle des corrélations. De plus, les données aberrantes ressortent encore mieux avec cette représentation.
4. Réaliser des ACP sur Rstat
Il existe différents moyens informatiques d’effectuer une analyse en composantes principales. Dans notre cas, nous allons nous intéresser aux solutions sous logiciel libre R.
Pour effectuer une ACP sous logiciel R, vous pouvez ainsi utiliser différents packages : vegan, ade4, FactoMineR, Factoshiny… Dans cet article, nous nous attarderons sur les deux dernières solutions. J’ai découvert FactoMineR après la lecture du très bon article de Claire Della Vedova (lien rompu). Quant à Factoshiny, je m’y suis familiarisé grâce au tutoriel de François Husson.
L’exemple classique pour FactoMineR et Factoshiny est le fameux jeu de données « decathlon » inclus dans le package (rien à voir avec l’enseigne ! Il s’agit de la discipline sportive). J’ai pour ma part créé un jeu de données d’agro-environnement grâce au serveur Eurostat. J’ai baptisé mon fichier de données « agriculture.csv » et je l’importe dans le logiciel R :
agriculture = read.table(file = "agriculture.csv",
sep=";",dec=",",header=TRUE, row.names=1, check.names=FALSE)
La fonction summary(agriculture) permet de décrire ce jeu de données. La console R affiche les informations statistiques relatives aux 13 variables quantitatives présentes :
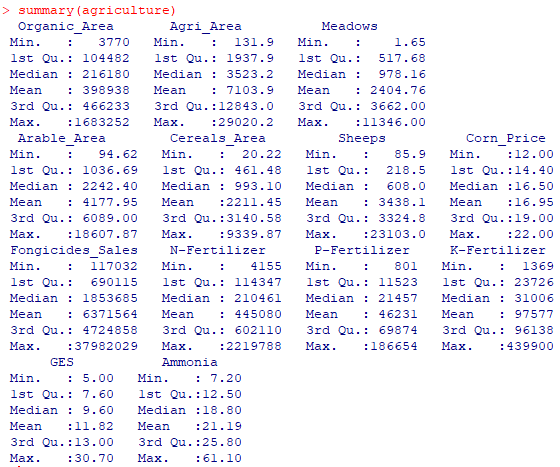
4.1. Générer une analyse ACP avec FactoMineR
Une fois le package chargé, je lance l’analyse :
agriculture.pca = PCA(agriculture[,2:5])
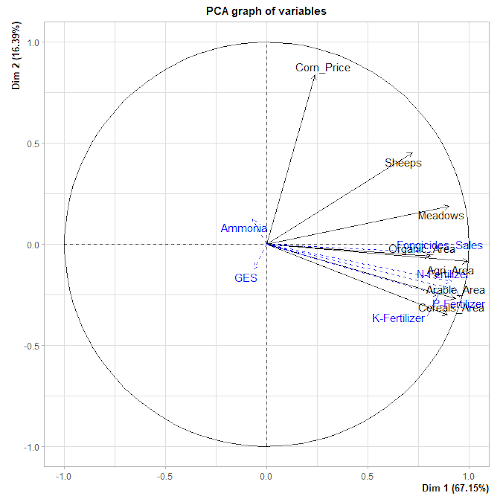
Le choix des données se voulait relativement hasardeux. Néanmoins nous retrouvons des corrélations logiques ! Ainsi le prix du maïs est indépendant des cultures de blé. A l’inverse, les corrélation entre fertilisation et surfaces cultivées sont positives.
Si vous obtenez seulement le graphique du cercle des corrélations, voici une astuce pour afficher également le graphique des observations. Il suffit de créer une nouvelle fenêtre graphique puis de relancer une commande graphique :
x11() plot(agriculture.pca)
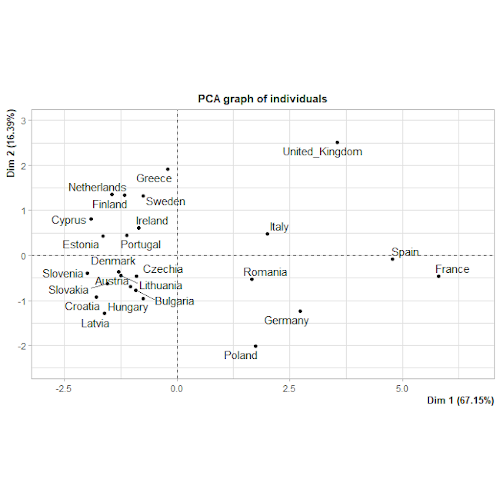
Pour obtenir plus d’informations sur l’analyse ACP, il suffit de rentrer la commande suivante :
summary(agriculture.pca)
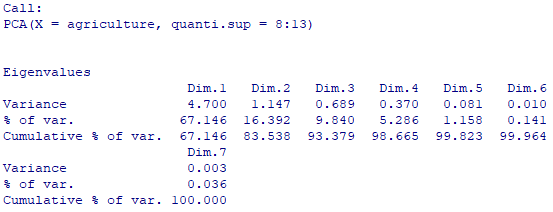
Les données s’affichent alors dans la console R.
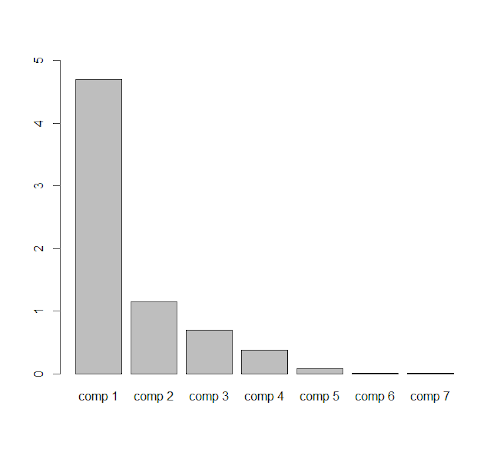
Il est également possible de visualiser graphiquement ces pourcentages d’inertie :
barplot(agriculture.pca$eig[,1],ylim=c(0,5))
4.2. Générer une analyse ACP avec Factoshiny
Le package Factoshiny propose de réaliser une analyse en composantes principales en passant par une interface de navigateur web. L’avantage de cette méthode repose sur les nombreuses options. Comme présenté plus haut, Factoshiny est détaillé dans le tutoriel de François Husson.
library(Factoshiny)
res = Factoshiny(agriculture)
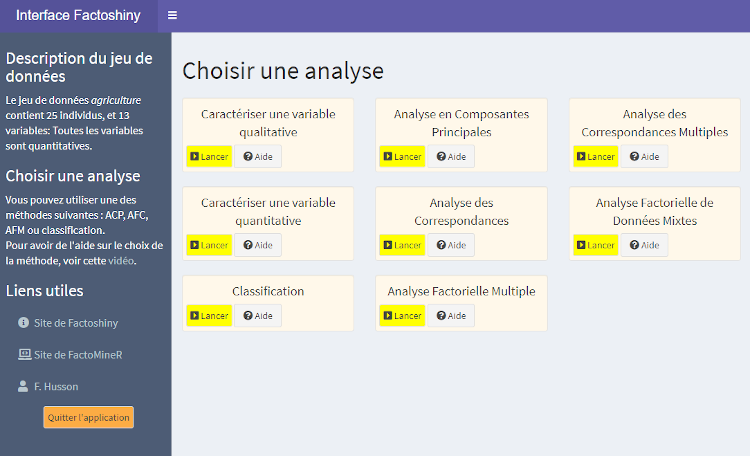
A noter que Factoshiny permet de télécharger des rapports automatiques ainsi que tous les graphiques générés (formats jpg, png, pdf).
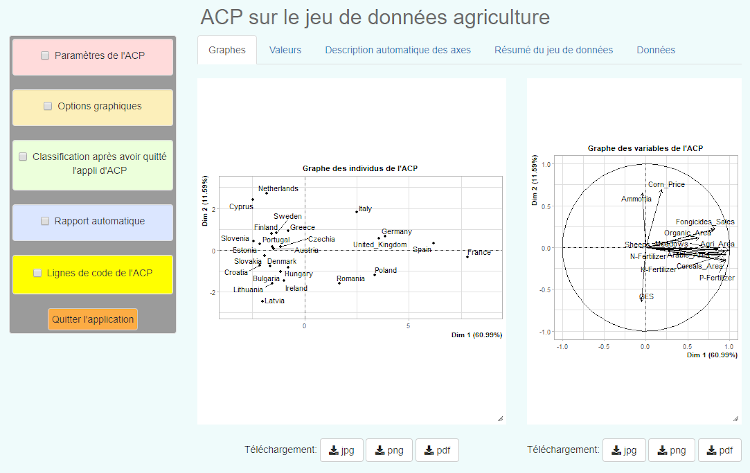
5. Les limites des analyses ACP en biologie ?
Peut-être lisez-vous cet article afin d’améliorer vos analyses de données en biologie. Il me faut cependant rajouter une section à cet article afin de modérer votre enthousiasme devant cet outil statistique. En effet, si les ACP permettent une exploration de vos données, leur utilisation nécessite quelques prudences. Une étude de 2022 montre ainsi que mal utilisées, les analyses ACP sont sources de biais d’interprétations. Entre 32000 et 216000 études de génétiques des populations seraient ainsi à réévaluer ! Un véritable pavé dans la mare, et pour cause : l’ACP permet une première exploration des données, s’y limiter avant de conclure présente donc un risque d’interprétation biaisée.





