Tout le monde ou presque connaît la régression linéaire. Il s’agit du traitement statistique le plus employé en sciences, notamment via le logiciel MS Excel. Mais bien souvent, les données terrain ne suivent pas de modèle pré-programmé. L’utilisateur que nous sommes tente alors d’appliquer les fonctions d’estimation proposées, sans réelle conviction.
Le logiciel R propose quant à lui d’effectuer des régressions non-paramétriques. Ces solutions sont bien plus intéressantes car elles permettent d’obtenir, en très peu de lignes de commande, un graphique complet avec sa courbe de tendance. Revers de la médaille, il faut beaucoup de points pour obtenir une estimation pertinente. A travers un exemple simple, le nombre de données de Pouillot à grands sourcils (Phylloscopus inornatus) observés en Bretagne ces vingt dernières années, je vous propose d’en découvrir plus sur ces possibilités statistiques de R.
1. Introduction à la régression non-paramétrique
En analyse de données, la régression désigne un ensemble de méthodes statistiques permettant de relier entre-elles deux variables x et y selon une fonction d’estimation. Le cas le plus connu est bien entendu la régression linéaire et sa méthode des moindres carrés. Il s’agit alors de déterminer une droite passant le « plus au milieu » du nuage de points. Le modèle prend en compte la dispersion du nuage de points et calcule les coefficients estimés (a,b) pour la droite d’équation de type y = a.x + b.
La régression linéaire appartient elle-même à une catégorie dite des régressions paramétriques. Il s’agit de toute régression pour laquelle il existe une fonction d’estimation associée au modèle. Citons par exemple les régressions non-linéaires, ou bien encore les régressions polynomiales. Les calculs statistiques font alors apparaître un prédicteur f de paramètres connus, aussi appelé fonction d’estimation.
Mais comment procéder si l’on ignore quel prédicteur est le plus adapté, ou s’il n’existe pas de fonction d’estimation connue ? La solution consiste alors à faire appel à la régression non paramétrique. Il s’agit d’une forme d’analyse de la régression dans lequel le prédicteur, ou fonction d’estimation, ne prend pas de forme prédéterminée. Il se construit cependant à partir des données fournies. La situation la plus connue est le lissage de courbe, qui consiste à gommer les irrégularités du nuage de points.
Par conséquent, la régression non paramétrique exige des variables de plus grandes tailles que dans le cas de régression paramétriques. Tout simplement parce que les modèles de régression s’appuient sur directement sur les données. Plus le nuage de points est riche, plus la régression sera efficace.
2. Exemple d’application sous langage R
2.1. Données prises en compte : observations de Pouillot à Grands Sourcils en Bretagne
Avant de commencer, abordons tout d’abord le choix du jeu de données. Le Pouillot à grands sourcils (Phylloscopus inornatus) est un petit passereau de la famille des Phylloscopidés. Cet oiseau témoigne depuis quelques décennies d’un remarquable phénomène d’apparition d’une nouvelle route migratoire post-nuptiale. En effet, ce nicheur sibérien et nord-asiatique hiverne en Asie du sud-est, dans une bande couvrant le Bengladesh jusqu’à la Malaisie. Sa route migratoire traditionnelle contourne l’Himalaya par l’est, soit pour les nicheurs les plus occidentaux un périple de plus de 8000 km !
A partir des données collectées sur Faune-Bretagne, il est possible de réaliser un graphique des observations sur ces vingt dernières années, et ainsi d’en déduire des tendances reflétant l’apparition actuelle de cette nouvelle route migratoire. Les données sont compilées dans un fichier PGS.csv qui est facilement importé sous R. Il ne reste plus qu’à réaliser un graphique associé à une régression non-paramétrique.
PGS=read.table(file="PGS.csv",sep=";",header=TRUE)
names(PGS)
[1] "Year" "Bretagne" "LoireAtlantique" "Vendee"

2.2. Régression non-paramétrique sous R
Les commandes basiques de R permettent d’effectuer des régressions non-paramétriques. Commençons tout d’abord par utiliser la fonction loess() :
lissage=loess(Bretagne~Year)
Il faut ensuite récupérer les données du lissage. La fonction predict() est une fonction générique de R pour obtenir des prédictions à partir des résultats de diverses fonctions d’ajustement de modèle. Nous allons enregistrer ces résultats dans l’objet yfit.
yfit=predict(lissage, newdata=Year)
Nous pouvons ensuite générer le graphique ainsi que la courbe de régression non-paramétrique :
plot(Year,Bretagne,main="Nombre de
données de Pouillot à Grands Sourcils \n par année d'observation", pch=17)
lines(Year,yfit, col="#c26f10",lty=2, lwd=2)
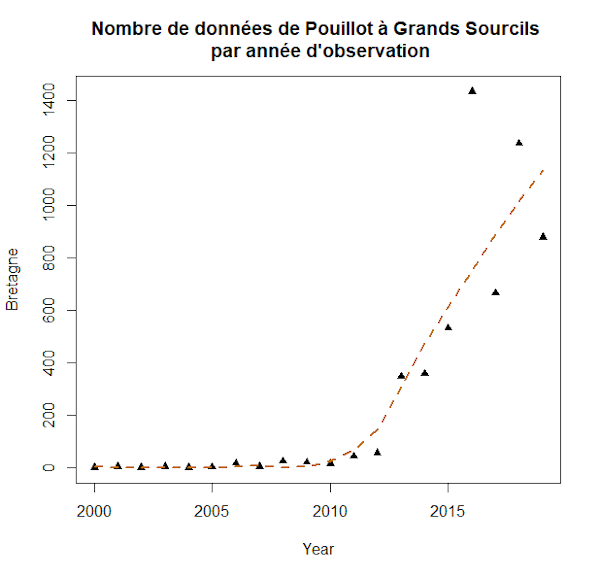
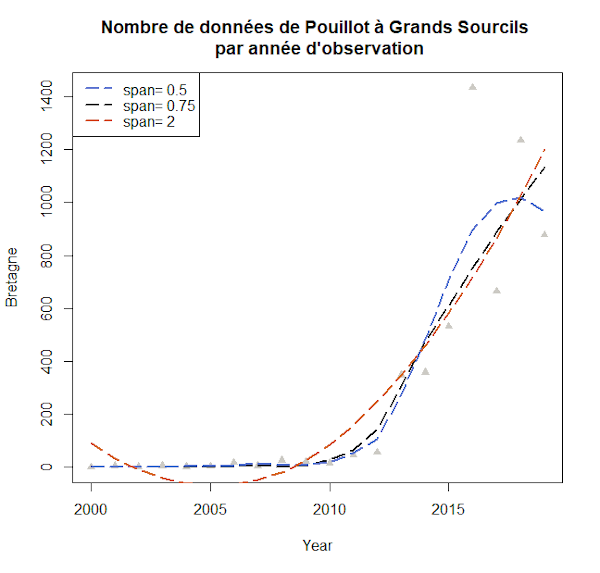
Le paramètre span de la fonction loess() permet d’accentuer le lissage. Par défaut, span=0.75 et cette valeur est appliquée par R si le paramètre n’est pas renseigné. De plus, une valeur faible va augmenter la sensibilité du lissage. Enfin pour aller plus loin avec la régression non-paramétrique sous R, je vous conseille de visiter ce lien.
plot(Year,Bretagne,main="Nombre de
données de Pouillot à Grands Sourcils \n par année d'observation",
pch=17, col="#cccac4")
#Prédiction des valeurs du modèle d'ajustement pour trois paramètres span :
yfit2=predict(loess(Bretagne~Year,span=2),newdata=Year)
yfit3=predict(loess(Bretagne~Year,span=0.5),newdata=Year)
yfit4=predict(loess(Bretagne~Year,span=0.75),newdata=Year)
#Tracé des courbes d'ajustement selon ces trois paramètres span :
lines(Year,yfit4, col="black",lty=5, lwd=2)
lines(Year,yfit3, col="#5a72d1",lty=5, lwd=2)
lines(Year,yfit2, col="#d6621a",lty=5, lwd=2)
#Légende du graphique :
legend("topleft",c(paste("span=",c(0.5,0.75,2))), lwd=2,lty=5,
col=c("#5a72d1","black","#d6621a"))
2.3. Le package ggplot2
Ce package d’extension graphique permet d’aller plus loin dans l’apparence des graphes sous R. Il propose également une fonction facilitant l’affichage des régressions linéaires ou non-paramétriques. Pour ces raisons, il peut être plus pratique d’utiliser ce package au lieu des fonctions basiques de R.
library(ggplot2)
theme_set(
theme_bw() +
theme(legend.position = "top") )
Il suffit ensuite d’utiliser la fonction qplot() disponible pour ce package afin d’afficher les données graphiques. En rajoutant la fonction geom_smooth() nous pouvons afficher la droite de régression associée à ce nuage de points :
qplot(y = Bretagne,x = Year, data = PGS) +
geom_smooth(method="line", se=FALSE)
Le package ggplot2 utilise une fonction bien plus complète pour générer des graphiques, il s’agit de ggplot() dont le fonctionnement est spécifique. En effet, elle utilise elle-même une fonction aes() afin de définir les valeurs des axes choisis dans un dataset cité en premier attribut. Comme elle ne fait que charger le jeu de données, il faut ensuite exécuter geom_point() afin d’afficher le graphique. Aussi avons-nous défini un objet PGSBretagne pour gagner du temps par la suite :
PGSBretagne <- ggplot(PGS, aes(Year, Bretagne)) +
geom_point()
Il ne reste plus qu’à exécuter l’objet PGSBretagne avec la fonction geom_smooth(). Ici, nous choisissons la méthode employée. par défaut, il s’agit de loess (régression non-paramétrique) mais il existe plusieurs valeurs possibles : lm, glm, gam, loess, rlm.
PGSBretagne + geom_smooth(method="loess")
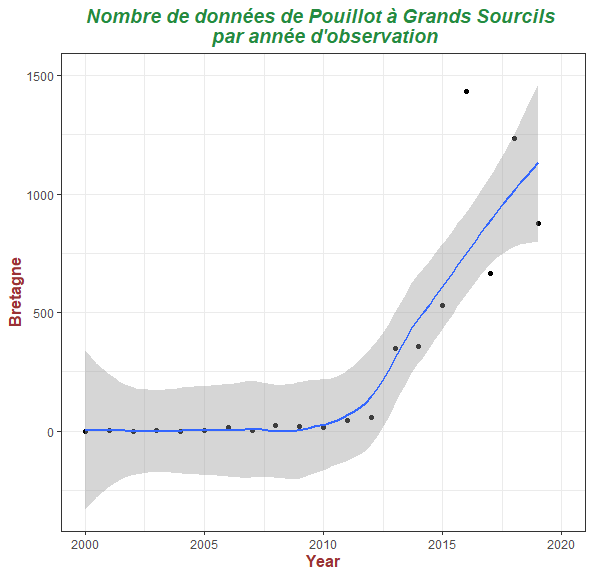
Pour le résultat final, nous avons un peu triché afin de jouer avec les possibilités graphiques de ggplot2. Voici donc le script complet du graphique ci-dessus :
PGSBretagne +
geom_smooth(method="loess",se = TRUE) + expand_limits(x=c(2000,2020),
y=c(0, 1500)) + ggtitle("Nombre de données de Pouillot à Grands
Sourcils \n par année d'observation") + theme(
plot.title = element_text(color="#258a40", size=14,
face="bold.italic",hjust = 0.5),
axis.title.x = element_text(color="#993333", size=12, face="bold"),
axis.title.y = element_text(color="#993333", size=12, face="bold"))





