Nous reviendrons ici sur les notions élémentaires en probabilités. Il s’agit en effet de réviser le socle indispensable de connaissances mathématiques, pour la plupart vues au lycée, nécessaires aux statistiques inférentielles.
Les lecteurs souhaitant plus de compléments d’information sur les probabilités sont donc invités à consulter des ouvrages de référence. Dans ce court chapitre, nous reviendrons donc sur quelques éléments d’analyse combinatoire et de probabilités que nul biostatisticien ne peut ignorer. Rien de bien compliqué, cette page servira surtout de révision rapide, histoire de se dérouiller.

2. Notions incontournables de probabilités
2.1. Notions d’analyse combinatoire
2.1.1. Principe multiplicatif
En mathématiques, le cardinal d’un élément E correspond au nombre d’éléments de E. Par exemple, il existe 21 acides aminés protéinogènes chez les Eucaryotes. Soit Card(Aa_Protéines) = 21.
Aussi à partir de deux ensembles finis A et B, le produit de A par B noté AB correspond à l’ensemble des couples (x, y) où x est le nombre d’éléments de A et y le nombre d’éléments de B, soit card(A.B) = card(A).card(B)
2.1.2. Arrangements sans répétition
Prenons le cas de figure de 3 amis qui décident d’aller chacun au cinéma voir un film différent à l’affiche sur les 5 que comptent la ville. Ils vont alors avoir 5x4x3 = 60 arrangements possibles de films vus durant cette soirée. Les objets de l’arrangement sont alors tous distincts. Le nombre d’arrangements sans répétitions de k objets parmi n objets est alors donné par la formule Akn = n!/(n-k)! . En effet, dans l’exemple précédent, nous obtenons 5!/(5-3)! = 60.
2.1.3. Arrangement avec répétition
Imaginons une molécule organique possédant k carbones asymétriques. Chaque configuration absolue donne deux énantiomères (n = 2). Le nombre de diastéréoisomères est alors de 2k. Nous sommes en présence d’un arrangement avec répétition de k objets parmi n objets : A = nk.
2.1.4. Permutations
Une permutation de n objets distincts est une suite ordonnée de ces n objets calculée par n! (factorielle n). Reprenons alors l’exemple des 21 acides aminés protéinogènes. Nous voulons constituer autant de peptides de 21 résidus exactement qu’il existe de permutations possibles de ces acides aminés. Nous pouvons donc envisager 21! permutations possibles, soit 5,109.1019 peptides possibles !
A noter que la permutation est un arrangement sans répétition de n objets pris dans n objets : Ann
2.1.5. Combinaisons
Dans l’exemple des amis au cinéma (arrangements sans répétition), nous considérions qu’il n’est pas équivalent que l’ami 1 voie le film A et l’ami 2 le film B; et que l’ami 2 voie le film B et l’ami 2 le film A. Or dans les combinaisons nous considérons que l’ordre dans la liste ne compte plus. Aussi il faut diviser par k! la formule de l’arrangement sans répétition pour enlever les combinaisons équivalentes.

2.2. Probabilités élémentaires
En mathématiques, l’espace fondamental Ω correspond à l’ensemble de tous les événements aléatoires dans l’univers des possibles. Un événement élémentaire ω est une action, une observation, une production (tirer une carte par exemple). La somme des événements élémentaires constitue l’événement A. Enfin, l’espace fondamental et ses événements est associé à l’épreuve ou l’expérience.
Aussi nous notons que ω ∈ A signifie la réalisation de l’événement A et que la notation Ᾱ est le complémentaire (≠) de A. Soit ω ∈ A ∉ Ᾱ . La probabilité P(A) = 1 – P(Ᾱ) si l’événement A est unique dans Ω .
De plus, si nous prenons en compte deux événements A et B, l’intersection entre ces deux événements est notée A∩B . S’ils sont disjoints ou incompatibles, alors A∩B = ∅ et la probabilité de leur réunion est P(A∪B) = P(A) + P(B) . Enfin, le principe d’indépendance des événements indique que P(A∩B) = P(A).P(B).
La réunion de deux événements quelconques A et B se formule aussi P(A∪B) = P(A) + P(B) – P(A∩B) . S’il existe plusieurs événements quelconques, leur réunion est donc la somme de leurs probabilités moins la somme des probabilités d’intersections respectives.
2.3. Probabilités combinatoires
Dans un espace fondamental Ω avec N événements élémentaires, le principe d’équiprobabilité d’un événement donne donc p = 1/N . Enfin, si k est le nombre de cas favorables à l’événement, alors p = k/N pour k ⊂ N.
2.4. Probabilités conditionnelles
2.4.1. Théorème de Bayes
Soit A et B deux événements de l’espace fondamental Ω avec P(B) ≠ 0 . On appelle alors probabilité conditionnelle de l’événement « A sachant B » la formule

De plus, les probabilités de relation entre A et B sont interchangeables car reliées à la probabilité de l’intersection des événements P(A∩B) :

Les lecteurs plus expérimentés en probabilités ne manqueront pas de signaler que la théorème de Bayes a une formulation plus complexe (version composée) lorsque sont considérés les partitions Bi de l’événement B dans l’espace fondamental Ω (formule des probabilités totales) :

Cette formule permet alors de calculer des événements plus complexes. Par exemple, la probabilité de répondre correctement à un jeu télévisé pour un candidat ayant le choix entre trois questions différentes (facile, moyenne, difficile).
2.4.2. Schéma de Bernoulli
Il s’agit de dresser un arbre de probabilités cumulant les épreuves indépendantes entre-elles où chaque nœud ne peut prendre que deux valeurs. Le schéma de Bernoulli est donc associé à une loi binomiale. Les probabilités de chaque événement se multiplient entre-eux le long de chaque branche (principe d’indépendance des événements).
Ces arbres peuvent ainsi considérer que le tirage est avec remise ou sans remise. Par exemple, ci-dessous un arbre avec remise à deux niveaux :
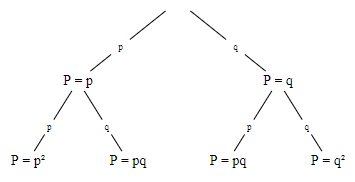
Quelle est la suite ? Dans l’épisode III, la revanche des variables aléatoires, nous explorerons ces applications mathématiques si cruciales en statistiques, puisqu’elles relient le monde des probabilités à la réalité des observations !





