Les statistiques en écologie, pour quoi faire, me direz-vous ? Et vous aurez bien raison. Etudier des statistiques pour le seul plaisir des chiffres n’est pas un loisir des plus exaltants. Mais le biologiste et l’écologue se retrouvent, bien malgré eux, obligés de maîtriser un minimum d’outils statistiques afin de triompher des montagnes de données collectées.
Pendant des années, les mathématiques et moi avons consommé un long divorce. Aucune thérapie de couple n’est parvenue à bout de cette crise et il a bien fallu me résoudre. Non, je n’ai pas la bosse des maths. Mais si comme moi vous partagez cet horrible complexe, rassurez-vous ! D’après le psychologue Howard Gardner, il existerait huit formes d’intelligences. Ainsi ce bon Dr Gardner distingue l’intelligence naturaliste de l’intelligence logico-mathématique ! Voilà notre égo sauvé et les orgueilleux matheux remis à leur place.
Alors si comme moi vous vous sentez plus proche d’un Darwin que d’un Einstein (en toute modestie), excellente chose ! Vous êtes sur la bonne voie pour faire la paix avec les maths. Regardons-les telles qu’elles sont : de formidables outils. C’est précisément ce que nous allons explorer dans cette série d’articles. Alors, tel un inventaire à la Prévert, revenons ensemble sur les connaissances statistiques indispensables en écologie.

1. Les bases en statistiques descriptives
1.1. Les grandes définitions en statistiques
Un petit rappel tout d’abord. Les probabilités théorisent et permettent de modéliser des phénomènes aléatoires. Les statistiques reposent sur l’observation de données issues d’un phénomène concret. Dans un cas nous théorisons, dans l’autre cas nous observons. Or ce n’est pas parce que nous observons un phénomène que nous ne pouvons pas formuler d’hypothèses, ni conclure ! Il existe d’ailleurs deux grands domaines de statistiques : les statistiques descriptives et les statistiques décisionnelles.
Les statistiques descriptives décrivent les données, les analysent et suggèrent des relations. Les statisticiens proposent des méthodes avancées d’analyses des données. Comme classer et subdiviser les populations en groupes homogènes (partitonnement, CAH). Ou encore résumer les caractéristiques d’une population en composantes synthétiques potentiellement pertinentes (méthodes d’analyse factorielle : ACP, AFCM…).
Les statistiques décisionnelles (ou inférentielles) considèrent la série de données comme un échantillon n d’une population N. Il se pose alors la question de l’échantillonnage de n. A partir de là, elle vise à inférer les propriétés constatées de l’échantillon n à toute la population. Il faut ensuite confirmer ou informer les hypothèses formulées à l’aide de tests. Nous sommes ici dans dans le domaine des modèles statistiques. Les probabilités redeviennent prépondérantes.
1.2. Notions de statistiques descriptives
1.2.1. La population N et ses sous-ensembles
Nous avons vu précédemment que les statistiques organisent les données selon différents niveaux hiérarchiques. Un individu ou unité d’échantillonnage représente le plus bas niveau. C’est l’unité indivisible, la donnée considérée seule. L’ensemble des individus constitue la population N. Je peux associer à chaque individu de ma population des données ou variables spécifiques.
Par exemple, j’étudie toutes les N = 500 carottes de mon champ que je sacrifie pour connaître leur poids, la teneur en eau, le taux de pesticides accumulés, la teneur en carotène, etc… Ou alors, je décide qu’il serait plus sage d’échantillonner afin de vendre la majorité de ma récolte, et je choisis de sacrifier n = 20 carottes. Il s’agit alors d’un échantillon n qui est bien un sous-ensemble de N.
Tout l’art de la statistique décisionnelle sera donc de décrire la méthode d’échantillonnage (aléatoire, systématique, stratifiée…) pour que l’échantillon étudié ait le plus de chances possibles d’être représentatif de la population N.
1.2.2. Les types de variables
Dès lors, nous obtenons différentes données pour chaque individu. Mais tout dépend de ce que nous étudions. Les données associées à un individu sont appelées variables ou caractères statistiques. Il s’agit des séries de données d’un tableur, par exemple. Nous distinguons ainsi deux grands types de variables : qualitatives et quantitatives.
Les variables qualitatives sont des termes, noms, identités, descriptions non-chiffrées… Elles peuvent être nominales (indications) ou ordinales (notion de hiérarchisation).
Les variables quantitatives sont des chiffres. Elles peuvent être discrètes (l’ensemble des valeurs possibles est fini) ou continues (l’ensemble des valeurs possibles est infini).
1.3. Paramètres statistiques de description
La moyenne : le plus connu des paramètres statistiques. Elle permet d’indiquer la valeur moyenne calculée à partir des variables quantitatives prises en compte.

La médiane : moins fréquemment utilisée mais pourtant plus robuste, elle situe à partir de quelle variable 50% de la population est représentée.
Le mode : il donne la variable qui a la plus forte fréquence. Il peut s’agir de la médiane si la distribution des variables est symétrique.
Les quartiles (q1, q2 et q3) : ils indiquent à partir de quelles variables 25 % , 50 % puis 75 % de la population sont représentés. La médiane est donc un quartile (q2).
La représentation en « boîte à moustache » : une variable quantitative peut être graphiquement représentée à partir de ce modèle qui prend en compte le minimum, les quartiles (q1, q2 et q3) et le maximum. Un point supplémentaire peut indiquer la moyenne.
1.4. Paramètres statistiques de dispersion
Pour chaque jeu de données, il est essentiel de savoir si leur distribution est ordonnée ou au contraire aléatoire. De cette évaluation de la dispersion, nous pourrons par la suite en tirer des informations utiles.
Les espaces inter-quartiles : ils mesurent la dispersion au sein de la boîte à moustache.
L’étendue : c’est la différence entre les valeurs maximales et minimales. En représentation graphique, on considère que l’étendue dans une boîte à moustache ne doit pas être supérieure à 1,5.(q3-q1) .
La variance : elle permet d’évaluer la dispersion dans la population. En mathématiques, elle se calcule comme la moyenne des carrés des écarts à la moyenne. Cela signifie qu’elle se détermine en faisant la somme des différences au carré entre variable et moyenne pour chaque individu de la série, puis que cette somme est divisée par le nombre d’individus.

C’est pourquoi la variance est toujours positive et ne peut qu’augmenter avec l’écart à la moyenne. Cependant, elle présente deux défauts : son unité est au carré (ce qui la rend moins facile d’interprétation) et sa valeur peut devenir rapidement trop forte (pas vraiment parlant).
L’écart-type : pour les raisons évoquées au-dessus, l’écart-type est préféré à la variance afin d’évaluer la dispersion. Il s’agit de la racine carrée de la variance. Il est sans unités.

L’écart-type des moyennes : plus compliqué à comprendre, cet écart-type correspond à l’erreur générée par chaque tirage au sort d’un échantillon dans une population. Cela signifie que pour une variable, à chaque fois qu’un échantillon est étudié, nous obtenons une nouvelle moyenne. Il apparaît donc une dispersion entre ces moyennes alors que nous répétons l’échantillonnage. Cela nous donne l’écart-type des moyennes ou erreur standard (e.s.). Cette valeur est très utilisée en biologie, car elle sert à définir les barres d’erreur sur les graphiques de résultats.

Le coefficient de variation, ou écart type relatif, est une mesure de dispersion relative. Il s’agit du rapport entre l’écart-type et la moyenne selon la formule Cv = σ/µ . Ce coefficient est sans unités et parfois exprimé en pourcentages.
1.5. La covariance, paramètre de liaison entre deux séries quantitatives
1.5.1. La covariance Cov(X,Y)
Un graphique d’axes X,Y représente la répartition des individus rapportés selon deux variables quantitatives. Nous avons par exemple indiqué pour chaque poisson pêché le poids (abscisses) et la taille (ordonnées). Nous cherchons à examiner si la dispersion est importante le long de ces axes. Pour cela, il faut effectuer un calcul de covariance qui va prendre en compte l’étalement et l’inclinaison du nuage de points.
La covariance Cov(X,Y) entre deux variables quantitatives X et Y est le calcul de leurs écarts conjoints par rapport à leurs moyennes respectives. La covariance est toujours une comparaison entre les variances de deux variables. De sorte que la covariance d’une variable sur elle-même équivaut à Cov(X,X) = Var(X).
S’il existe 2 ou plus séries de variables quantitatives alors la covariance s’exprime comme un tableau algébrique des covariances possibles entre variables. Toutes les combinaisons sont ainsi prises en compte. Ce tableau s’appelle plus précisément une matrice de covariance.
Cette façon de procéder permet ensuite au statisticien de programmer des outils dits d’analyse multivariée comme l’Analyse en Composantes Principales (ACP), très utilisée pour rechercher des corrélations entre différentes séries de données. Cette matrice de covariance est fondamentale en Data Mining par exemple.
1.5.2. Comment interpréter une covariance Cov(X,Y) ?
La covariance permet de déterminer des tendances entre les deux variables quantitatives suivies. En effet, si la covariance est nulle, alors la répartition des points est aléatoire. Si elle est positive ou négative, alors elle révèle une proportionnalité entre les deux variables. Ceci se traduit graphiquement de la manière suivante : ci-dessous, des séries de variables fictives X et Y ont été représentées par rapport aux écarts respectifs à la moyenne pour chaque valeur.
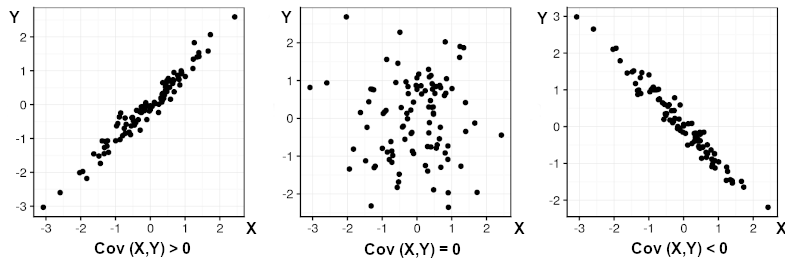
Les allures obtenues illustrent que le signe de la covariance Cov(X,Y) permet d’interpréter la relation entre les deux variables.
1.5.3. Comment interpréter un coefficient de corrélation linéaire ?
Nous avons observé pour chaque individu deux variables quantitatives. Le signe arithmétique de la covariance permet de noter qu’il existe une proportionnalité entre les deux variables X,Y.
Mais les valeurs de covariance ne sont pas normées. C’est à dire que leur valeur peut augmenter ou diminuer selon les données, sans qu’il soit possible d’en déduire que la corrélation obtenue soit plus forte ou plus faible.
Afin de décrire plus efficacement une corrélation, il nous faut calculer le coefficient de corrélation linéaire r (Pearson). Cette mesure est normée de telle sorte que la corrélation positive est comprise entre r = ]0;+1] et la corrélation négative est comprise entre r = [-1;0[ . Plus la valeur étant proche de -1 ou 1, plus la corrélation est parfaite.

1.6. Exemple de statistiques : une classe d’école
1.6.1. Une histoire de statistiques sur cahier de liaison
Dans une classe de 30 élèves (N = 30), le professeur de mathématiques dresse un tableau-bilan. Il note les prénoms de chaque élève (variables qualitatives nominales), précise leur moyenne (variable quantitative discrète entre 0 et 20), indique s’ils sont un peu, beaucoup ou pas du tout attentifs (variable qualitative ordinale) et s’amuse à rajouter leur taille (variable qualitative continue). Enfin, il se demande aussi comment le temps passé devant les écrans influence les résultats scolaires. Il demande donc aux parents d’indiquer sur le cahier de liaison le nombre d’heures journalières que leurs chers bambins consacrent aux écrans (variable quantitative discrète).
Nous avons donc un tableau de données avec quatre variables différentes. A partir du logiciel statistique R, nous effectuons un résumé statistique de la variable « Moyenne » ainsi que sa représentation en « boîte à moustache » . Le logiciel nous renvoie les informations suivantes :
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.00 10.12 12.00 11.93 13.88 20.00
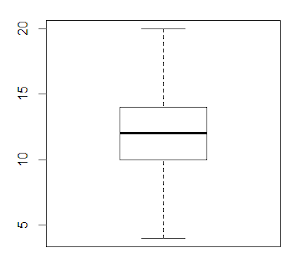
1.6.2. La covariance n’est pas toujours corrélation
Il se demande ensuite s’il existe une relation entre la moyenne de classe et la taille de ses élèves. Sous le logiciel R, nous effectuons le graphique plot(Moyenne, Taille) :
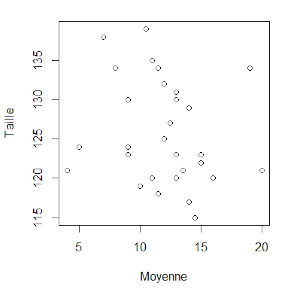
A première vue, il ne semble pas vraiment y avoir de relation entre ces deux variables. Calculons sous R la covariance Cov(Moyenne, Taille) et le coefficient de corrélation linéaire r entre ces deux variables (voir section 1.5) :
cov(Moyenne, Taille)
[1] -4.117241
cor(Moyenne, Taille)
[1] -0.1794513
Premièrement, la covariance est de signe négatif, nous pouvons en déduire une corrélation négative. Mais est-elle significative pour autant ? Deuxièmement, le coefficient de corrélation est très faible car r = -0,179 ! Le logiciel nous met donc en garde sur la grande faiblesse d’une corrélation entre taille et moyenne de classe…
1.6.3. Un dernier exemple de corrélation sous R
Notre professeur se demande ensuite si le temps quotidien passé devant les écrans n’influence pas les résultats scolaires. Sous R, nous effectuons le graphique plot(Ecrans, Moyenne) :
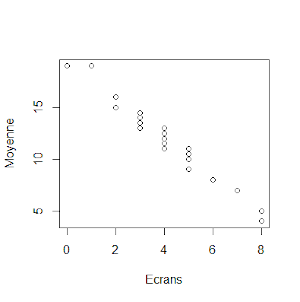
En effet, il semble exister une corrélation ! Vérifions-le comme précédemment :
cov(Ecrans, Moyenne)
[1] -6.013793
cor(Ecrans, Moyenne)
[1] -0.9777838
Le coefficient de corrélation est donc très fort car r = -0,977 ! Notez que le logiciel R indique un coefficient négatif en raison de la nature de la corrélation (négative). En conclusion, notre professeur rajoute un mot à tous les parents dans le cahier de liaison. S’ils veulent améliorer la moyenne de maths de leurs chères têtes blondes, alors sus aux écrans !
Quelle est la suite ? Dans l’épisode II, l’attaque des probabilités, nous reviendrons sur les notions élémentaires indispensables pour comprendre les statistiques inférentielles. Comme vous le verrez, rien de bien difficile, mais quelques rappels salutaires pour la suite des événements !





